Solve optimization problems in Jupyter Notebooks

For this course, our Jupyter Notebooks follow the same structure for all problems by defining the following sections:

• Import libraries

• Define variables

• Define objective function

• Define constrain function(s) if needed

• Solve the problem

• Postprocess results if needed

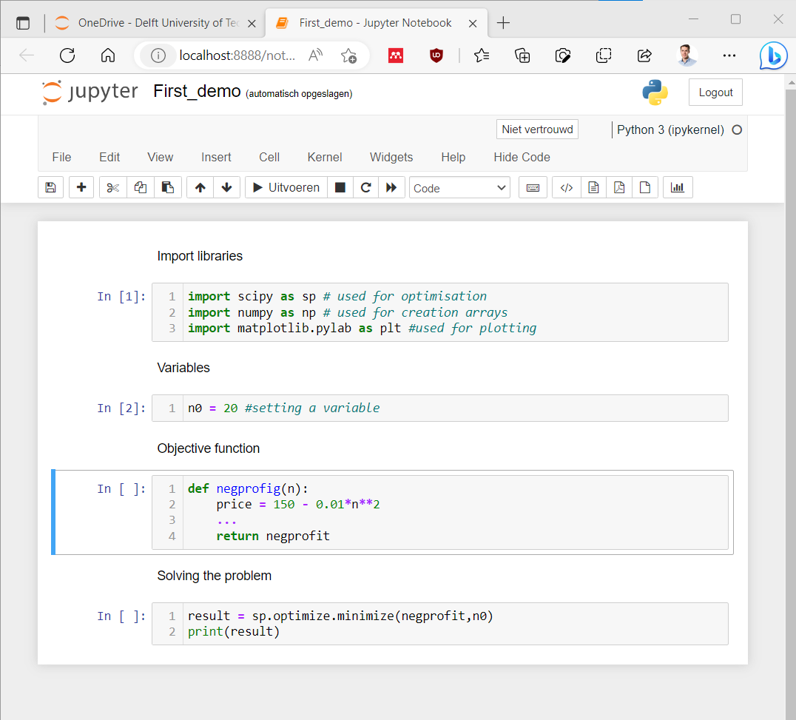
Fig. 5 General layout Jupyter Notebooks in this course

The structure is shown for an example which will be treated in-depth later.

Import libraries

Python cannot do optimization on its own, therefore we make use of separate packages which are installed with Anaconda:

• scipy used for optimization

• numpy used for matrix algebra

• matplotlib used for plotting

Libraries are imported with import ... as ... which directly abbreviates the packages for later use.

import scipy as sp
import numpy as np
import matplotlib.pylab as plt

Test Yourself

Define variables

In this part of the notebook we can store all our variables in the form of integers, floats and arrays.

n0 = 20

Test Yourself

Define objective function

In this part we define our constraint function as a callable with def ...: ... return ... These functions can contain multiple lines of calculation but should return one values which is minimized.

def negprofit(n):
    price = 150 - 0.01 * n**2
    revenues = price * n
    totalcost = 75 * n
    profit = revenues - totalcost
    return -profit

Test Yourself

Define constraint function

Similar to the objective function, the constrain function(s) can be defined, which may return multiple values

Solve the problem

Making using of the scipy-library, the problem is solved. Using print, the result is shown

result = sp.optimize.minimize(negprofit,n0)
print(result)

  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: -2499.9999999998727
        x: [ 5.000e+01]
      nit: 8
      jac: [ 0.000e+00]
 hess_inv: [[ 3.503e-01]]
     nfev: 22
     njev: 11

Postprocess results

If needed, we can postprocess the result or analyse the problem in another way

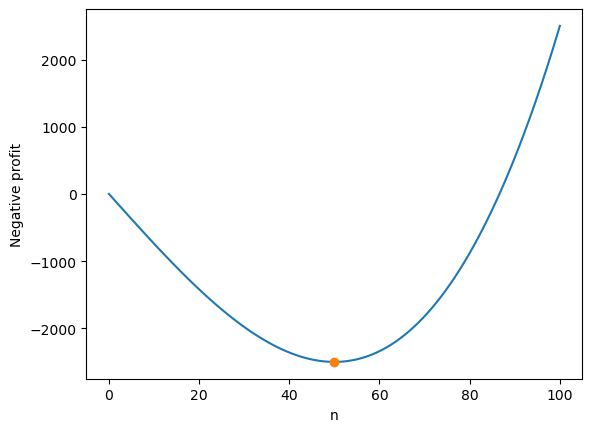
# checking the results with exhaustive search

n_range = np.linspace(0,100,100)
negprofit_result = negprofit(n_range)
plt.plot(n_range,negprofit_result)
plt.plot(result.x,result.fun,'o')
plt.xlabel('n')
plt.ylabel('Negative profit');

Test Yourself

Questions, discussions and comments