Mean Residual Life

Mean Residual Life#

One of the most popular techniques to select the threshold when performing POT is a graphical method called Mean Residual Life (MRL) plot1. MRL plot presents in the x-axis different values of \(th\) and, in the y-axis, the mean excess for that value of the \(th\). The range of appropriate threshold would be that where the mean excesses follows a linear trend.

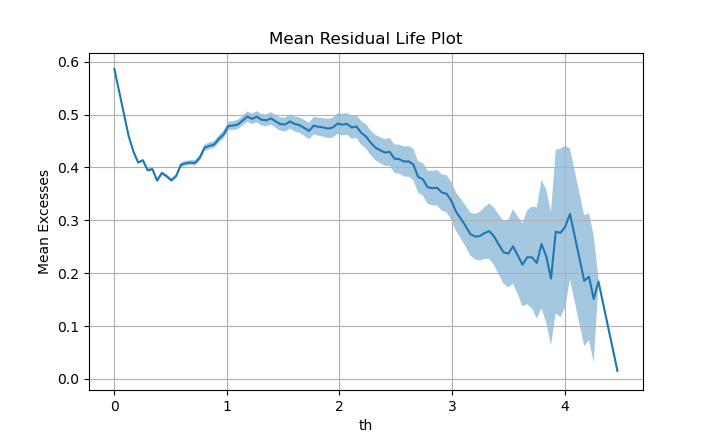
We have computed the MRL plot for our \(Hs\) data and we can see that there is a linear trend from \(H_s \approx 2m\) up to \(H_s \approx 3.5m\). Therefore, our selection of \(th=2.5m\) is appropriate according to the MRL plot. Note that this method is graphical, so it includes a bit of subjectivity.

../../_images/MRL_plot.png

But what is this based on?#

Let \(Y = [X-th|X>th]\) be the excesses above a threshold \(th\).

Let also \(Y\) be Generalized Pareto (GPD) distributed.

Thus, for every value of \(th^*\geq th\), the excesses \(Y^*= [X-th^*|X>th^*]\) are also GPD distributed with the same shape parameter, \(\xi\), a scale parameter \(\sigma_{th^*}=\sigma_{th}+\xi(th^*-th)\) and a mean value

\( \overline{Y}(th^*) = E[X-th^*|X>th^*] = \frac{\sigma_{th^*}}{1-\xi} \) 2

Introducing \(\sigma_{th^*}\) into the previous expression, we obtain

\( \overline{Y}(th^*)=\frac{\sigma_{th}+\xi(th^*-th)}{1-\xi}=Ath^*+B \)

being thus \(A=\frac{\xi}{1-\xi}\) and \(B=\frac{\sigma_{th}-\xi th}{1-\xi}\) the slope and intercept of a linear relationship. This means that a linear relationship exists between the mean excesses and the threshold selected when assuming a GPD. Therefore, if we plot the mean excess as function of the threshold, those parts of the plot where a linear relationship is observed are those where it is feasible to apply a GPD.

Let’s code it!#

In order to exemplify how to actually implement MRL plot, pseudo code is presented.

read observations

#define parameters
dl = 48 #in hours
range_thresholds = linspace(min, max, step)

for i in length(range_thresholds):
    excesses = find_peaks(observations, threshold = th[i], distance = dl) - th[i]
    mean_excesses[i] = mean(excesses)

plot(x = range_threshold, y = mean_excesses)
1

Davison and Smith (1990). Models for exceedances over high thresholds, journal of the royal statistical society. Journal of the Royal Statistical Society. Series B (Methodological), 52(3), 393-442.

2

The expectation of \(X \sim GPD\) is computed as \(E[X]=\mu+\frac{\sigma_{th}}{1-\xi}\)

Contents