Maximum bending moment on a simply supported bridge#
Example#
A 12 m span bridge is modelled as 1D continuous simply supported beam. The bridge is subjected to the axle loads (\(A\)) of 3-axle vehicle, as shown in the figure bellow. The largest axle load will generally cause the maximum bending bending moment (\(M_{max}\)) under its location \(p\).
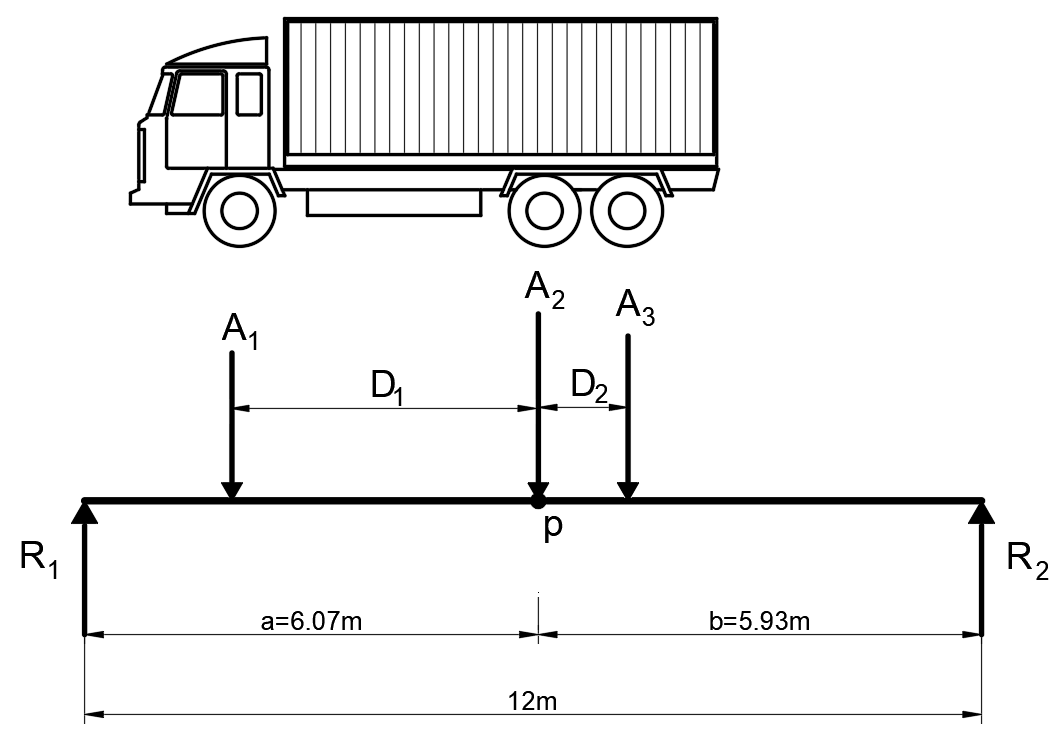
For this particular vehicle characteristics, i.e., \(A_1 \leq A_3 \leq A_2\) and \( D_2 \leq D_1 \leq a\). \(M_{max}\) can be computed as follows:
\(M_{max} = R_1 a-A_1D_1\)
\(R_1 = \frac{\left ( \sum_{i=1}^{3}A_i \right )a}{L}, \; i=\{1,2,3\}\)
where \(R_1\) is the reaction at the left side of the beam, \(L\) the total span length, \(A_i\) is the individual axle load \(i\), \(D_i\) corresponds to the inter-axle distance \(i\) and \(a\) is the distance at which the point of interest \(p\) is located.
For this example, we will use a sample of 100 vehicles corresponding to the 3-axle vehicle type 3C. The measurements were taken by the Weigh-in-Motion (WIM) system on the federal highway BR-101, located in the south of Brazil, in April 2014. The data collected through WIM system includes type of vehicle, individual axle loads and individual inter-axle distances.
We will determine:
The mean value of \(M_{max}\) at the point \(p\) of the beam.
The characteristics of the vehicle that cause the minimum \(M_{max}\) at the point \(p\) of the beam.
The characteristics of the vehicle that cause the maximum \(M_{max}\) at the point \(p\) of the beam.
Solution#
We start by importing numpy and loading the data set.
import numpy as np
data = np.loadtxt("https://raw.githubusercontent.com/TUDelft-CITG"
"/learn-python/mike/book/05/Exercises/02_01.csv",
delimiter=",",
skiprows=1,
)
print(
f"The shape of data is {np.shape(data)}.\n"
f"Hence, there are {np.shape(data)[0]} rows and"
f"{np.shape(data)[1]} columns in data.\n"
)
print(f"The first 5 rows of the data array are:\n\n {data[0:5,:]}")
The shape of data is (100, 5).
Hence, there are 100 rows and5 columns in data.
The first 5 rows of the data array are:
[[42.1 77.5 65.3 5.1 1.4]
[48.7 80.1 50.2 5.4 1.2]
[51.7 90.2 61.6 5.2 1.2]
[41.2 75.7 58.6 5.4 1.2]
[25. 48.4 33.5 5.6 1.2]]
Let’s break it down
To load the data set with numpy we use np.loadtxt() using the parameters delimiter="," to define the character used to separate the values and skiprows=1 to skip the first line.
The first 3 columns of the data set correspond to the axle loads and the remaining columns to the inter-axle distances. The data units are kN for the axle loads and m for the inter-axle distances.
Define the input variables to solve the problem and check if the conditions are satisfied.
span_length = 12 # [m]
distance_a = 6.07 # [m]
axle_loads = data[:, 0:3] # [kN]
inter_axle_distances = data[:, 3:5] # [m]
print("Do the characteristics of all vehicles meet the requirements?")
print("Is A2 > A3?", np.all(axle_loads[:, 1] > axle_loads[:, 2]))
print("Is A2 > A1?", np.all(axle_loads[:, 1] > axle_loads[:, 0]))
print("Is A3 > A2?", np.all(axle_loads[:, 2] > axle_loads[:, 0]))
print("Is a > D1?", np.all(distance_a > inter_axle_distances[:, 0]))
print(
"Is D1 > D2?", np.all(inter_axle_distances[:, 0] > inter_axle_distances[:, 1])
)
Do the characteristics of all vehicles meet the requirements?
Is A2 > A3? True
Is A2 > A1? True
Is A3 > A2? True
Is a > D1? True
Is D1 > D2? True
Let’s break it down
Here’s a step-by-step explanation of the code:
This code sets up geometric characteristics for a bridge, including the span length and the distance a at which a point of interest is located.
It then extracts axle load and inter-axle distance observations from a data source, with axle loads stored in the
axle_loadsvariable and inter-axle distances stored in theinter_axle_distancesvariable.Next, it prints a message asking whether the characteristics of all vehicles meet the requirements. It then uses numpy’s
np.all()function to compare the values in the second column (\(A_2\)) of theaxle_loadsarray with the values in the third column (\(A_3\)), checking if \(A_2\) is greater than \(A_3\) for all rows. The result of this comparison is printed as a boolean value, indicating whether the condition isTrueorFalse.Lastly, performs the same computations as in step 3 for the remaining requirements.
Use the given equations to compute the \(M_{max}\) caused by each one the vehicles in the data.
reaction_1 = (np.sum(axle_loads, axis=1) * distance_a) / span_length
max_bending_moment = reaction_1 * distance_a - axle_loads[:, 0] * inter_axle_distances[:, 0]
Answering the first question: What is the mean value of \(M_{max}\) at the point \(p\) of the beam.
mean_max_bending_moment = np.mean(max_bending_moment)
print(
f"The mean maximum bending moment is "
f"{mean_max_bending_moment:.2f}kNm"
)
The mean maximum bending moment is 328.88kNm
Answering the second question: What are the characteristics of the vehicle that cause the minimum \(M_{max}\) at the point \(p\) of the beam?
min_max_bending_moment = np.min(max_bending_moment)
idx_min_max_bending_moment = np.argmin(max_bending_moment)
vehicle_min_max_bending_moment = data[idx_min_max_bending_moment]
print(
f"The vehicle that causes the min bending moment of {min_max_bending_moment:.2f} "
f"kNm is the vehicle number {idx_min_max_bending_moment}\n"
f"With axle loads: {vehicle_min_max_bending_moment[0:3]} in kN\n"
f"and inter-axle distances: {vehicle_min_max_bending_moment[3:5]} in m \n"
)
The vehicle that causes the min bending moment of 133.73 kNm is the vehicle number 15
With axle loads: [24.9 39.3 27.2] in kN
and inter-axle distances: [5.9 1.2] in m
Answering the second question: What are the characteristics of the vehicle that cause the minimum \(M_{max}\) at the point \(p\) of the beam?
max_max_bending_moment = np.max(max_bending_moment)
idx_max_max_bending_moment = np.argmax(max_bending_moment)
vehicle_max_max_bending_moment = data[idx_max_max_bending_moment]
print(
f"The vehicle that causes the max bending moment of {max_max_bending_moment:.2f}"
f" kNm is the vehicle number {idx_max_max_bending_moment}\n"
f"With axle loads: {vehicle_max_max_bending_moment[0:3]} in kN\n"
f"and inter-axle distances: {vehicle_max_max_bending_moment[3:5]} in m \n"
)
The vehicle that causes the max bending moment of 582.44 kNm is the vehicle number 48
With axle loads: [ 62.5 117.7 107.2] in kN
and inter-axle distances: [4.8 1.2] in m
Exercise#
Get the largest element of each column of the WIM sample provided above to create the synthetic vehicle 3C Magnus. Using the same dimensions of the previous described bridge answer the following questions:
What is the value of last axle load \(A_3\) of the Maximum truck?
What is the value of the bending moment at the point \(p\) of the beam caused by the Maximum truck?
Toolbox
Here is your toolbox to solve this exercise:
Import numpy and load the data set.
Define the input variables and check if the conditions are satisfied.
Get the maxim values of the axle loads and inter-axle distances to create the synthetic vehicle.
Use the given equations on the example to compute \(M_{max}\) caused by the synthetic vehicle.
You can use the following numpy functions (but not limited to):
np.loadtxt(), np.all(), np.max()
Jupyter Lite session
Start a Jupiter lite session here to open a new tab where you can freely write and run your code.
Wait until the message “You may begin!” is printed.
Note: use the following line to load the data file:
data = np.loadtxt('/drive/data/02_01.csv',delimiter=',',skiprows=1)
