5.2. Doorsnedegrootheden

Definitie doorsnedegrootheden

oppervlakte	statische moment	traagheids- moment	polair traagheids- moment	verschuivingsregel van Steiner
\(\mathsf{A = \int _{A} dA}\)	\(\mathsf{S_y = \int_A y \cdot dA}\)	\(\mathsf{I_{yy} = \int_A y^2 \cdot dA}\)	\(\mathsf{I_p=\int_A r^2 \cdot dA = I_{yy} + I_{zz}}\)	\(\mathsf{I_{\overline{y}\overline{y}} = I_{yy(eigen)} + \overline{y}^2_C \cdot A}\)
	\(\mathsf{S_z = \int_A z \cdot dA}\)	\(\mathsf{I_{yz} = I_{zy} = \int_{A}y \cdot z \cdot dA }\)		\(\mathsf{I_{\overline{y}\overline{z}} = I_{\overline{z}\overline{y}} = I_{yz(eigen)} + \overline{y}_C \cdot \overline{Z}_C \cdot A}\)
		\(\mathsf{I_{zz} = \int_{A}z^2 \cdot dA}\)		\(\mathsf{I_{\overline{z}\overline{z}} = I_{zz(eigen)} + \overline{z}^2_C \cdot A}\)

Doorsnedegrootheden

vorm	oppervlakte, coördinaat zwaartepunt C	traagheidsmoment eigen	traagheidsmoment andere
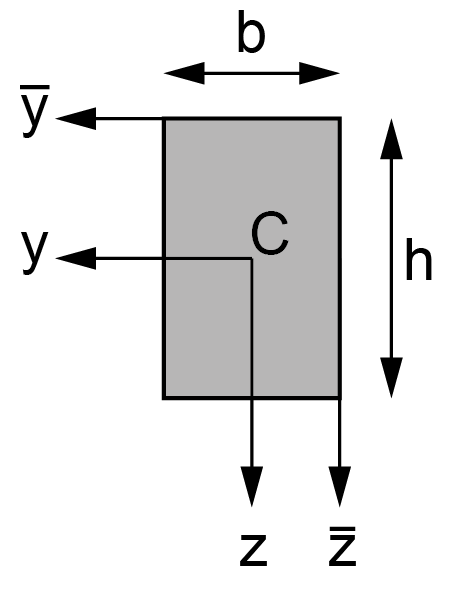
rechthoek	\(\mathsf{A=bh}\) \(\mathsf{\overline{y}_C = \frac{1}{2}b}\) \(\mathsf{\overline{z}_C = \frac{1}{2}h}\)	\(\mathsf{I_{yy}=\frac{1}{12}b^3h}\) \(\mathsf{I_{zz} = \frac{1}{12}bh^3}\) \(\mathsf{I_{yz} = 0}\)	\(\mathsf{I_{\overline{y}\overline{y}}=\frac{1}{3}b^3h}\) \(\mathsf{I_{\overline{z}\overline{z}}=\frac{1}{3}bh^3}\) \(\mathsf{I_{\overline{y}\overline{z}}=\frac{1}{4}b^2h^2}\)
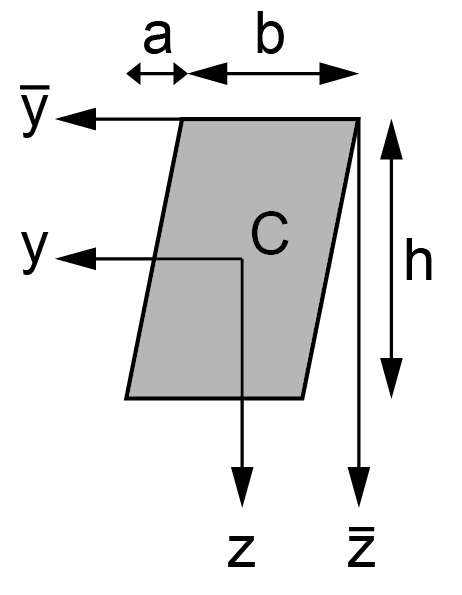
parallelogram	\(\mathsf{A=bh}\) \(\mathsf{\overline{y}_C = \frac{1}{2}(a+b)}\) \(\mathsf{\overline{z}_C = \frac{1}{2}h}\)	\(\mathsf{I_{yy}=\frac{1}{12}(a^2+b^2)bh}\) \(\mathsf{I_{zz} = \frac{1}{12}bh^3}\)	\(\mathsf{I_{\overline{z}\overline{z}}=\frac{1}{3}bh^3}\) \(\mathsf{I_{yz} = \frac{1}{12}abh^2}\)
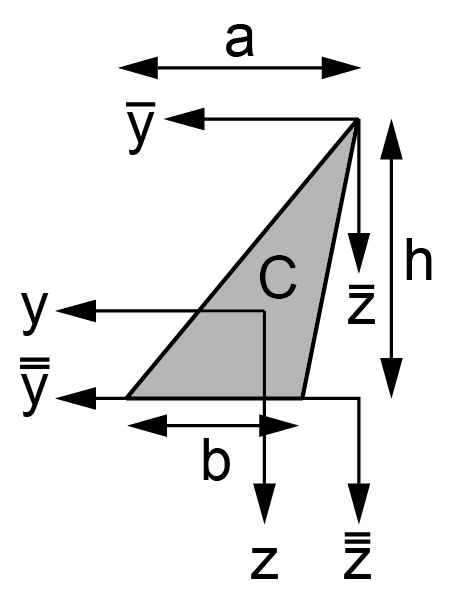
driehoek	\(\mathsf{A=\frac{1}{2}bh}\) \(\mathsf{\overline{y}_C = \frac{1}{3}(2a-b)}\) \(\mathsf{\overline{z}_C = \frac{2}{3}h}\)	\(\mathsf{I_{yy}=\frac{1}{36}(a^2-ab+b^2)bh}\) \(\mathsf{I_{zz} = \frac{1}{36}bh^3}\)	\(\mathsf{I_{\overline{z}\overline{z}}=\frac{1}{4}bh^3}\) \(\mathsf{I_{\overline{y}\overline{z}}=\frac{1}{8}(2a-b)bh^2}\) \(\mathsf{I_{yz} = \frac{1}{72}(2a-b)abh^2}\) \(\mathsf{I_{\overline{\overline{z}}\overline{\overline{z}}}=\frac{1}{12}bh^3}\)
trapezium	\(\mathsf{A=\frac{1}{2}(a+b)h}\) \(\mathsf{\overline{z}_C = \frac{1}{3}\frac{a+2b}{a+b}h}\)	\(\mathsf{I_{zz}=\frac{1}{36}\frac{a^2+4ab+b^2}{a+b}h^3}\)	\(\mathsf{I_{\overline{z}\overline{z}}=\frac{1}{12}(a+3b)h^3}\) \(\mathsf{I_{\overline{\overline{z}}\overline{\overline{z}}}=\frac{1}{17}(3a+b)h^3}\)
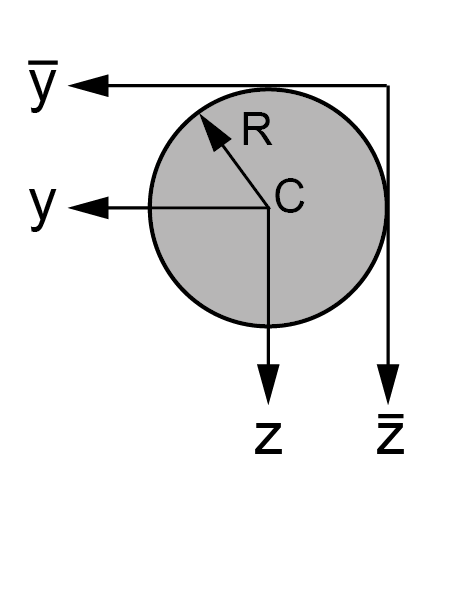
cirkel	\(\mathsf{A=\pi R^2}\)	\(\mathsf{I_{yy}=I_{zz}=\frac{1}{4}\pi R^4}\)	\(\mathsf{I_{\overline{y}\overline{y}}=I_{\overline{z}\overline{z}}=\frac{5}{4}\pi R^4}\) \(\mathsf{I_{yz}=0}\) \(\mathsf{I_{\overline{y}\overline{z}}=\pi R^4}\) \(\mathsf{I_p=\frac{1}{2}\pi R^4}\)
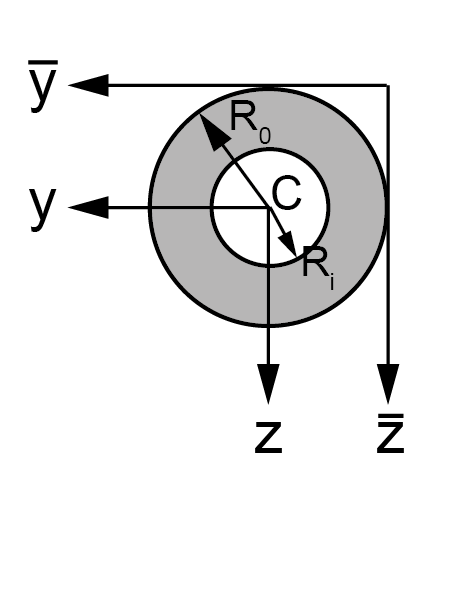
dikwandige ring	\(\mathsf{A=\pi (R_0^2-R^2_i)}\)	\(\mathsf{I_{yy}=I_{zz}=\frac{1}{4}\pi (R^4_0-R^4_i)}\)	\(\mathsf{I_{yz} = 0}\) \(\mathsf{I_p = \frac{1}{2}\pi (R^4_0 - R^4_i)}\)
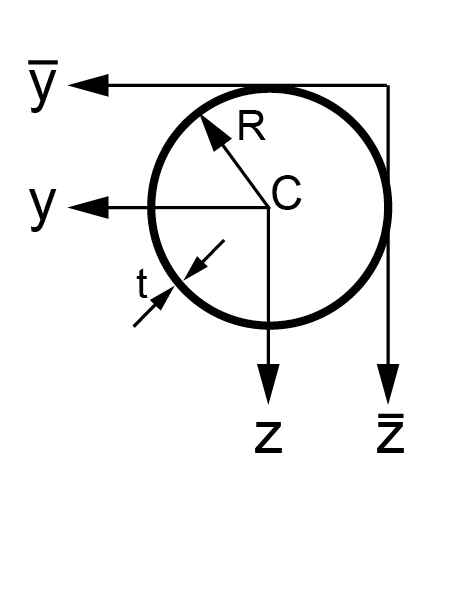
dunwandige ring	\(\mathsf{A=2\pi Rt}\)	\(\mathsf{I_{yy}=I_{zz}=\pi R^3t }\)	\(\mathsf{I_{\overline{y}\overline{y}}=I_{\overline{z}\overline{z}}=3\pi R^3t}\) \(\mathsf{I_{yz} = 0}\) \(\mathsf{I_p = 2\pi R^3t}\)
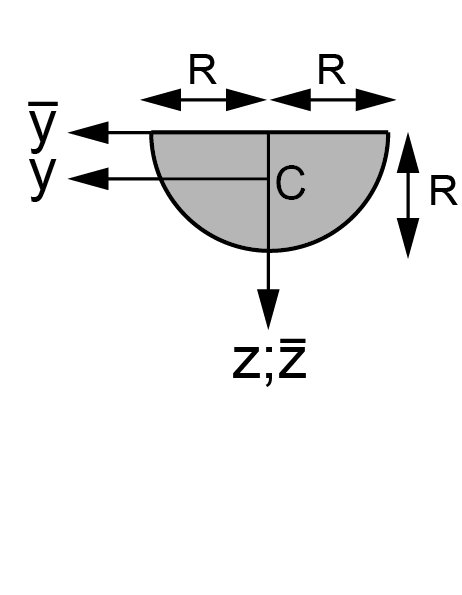
halve cirkel	\(\mathsf{A=\frac{1}{2}\pi R^2}\) \(\mathsf{\overline{y}_C = 0}\) \(\mathsf{\overline{z}_C = \frac{4}{3\pi}R}\)	\(\mathsf{I_{yy}=\frac{1}{8}\pi R^4 }\) \(\mathsf{I_{zz}=(\frac{\pi}{8}-\frac{8}{9\pi})R^4}\)	\(\mathsf{I_{\overline{y}\overline{y}}=I_{\overline{z}\overline{z}}=\frac{1}{8}\pi R^4}\) \(\mathsf{I_{\overline{y}\overline{z}}=0}\) \(\mathsf{I_{yz} = 0}\)
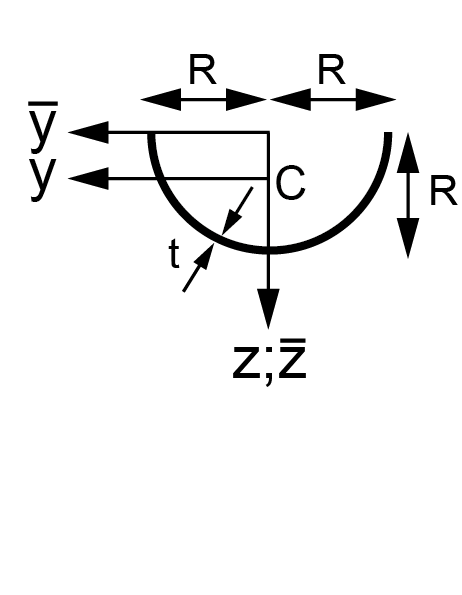
halve dunwandige ring	\(\mathsf{A=\pi Rt}\) \(\mathsf{\overline{y}_C = 0}\) \(\mathsf{\overline{z}_C = \frac{2}{\pi}R}\)	\(\mathsf{I_{yy}=\frac{1}{2}\pi R^3t }\) \(\mathsf{I_{zz}=(\frac{\pi}{2}-\frac{4}{\pi})R^3t}\)	\(\mathsf{I_{\overline{y}\overline{y}}=I_{\overline{z}\overline{z}}=\frac{1}{2}\pi R^3t}\) \(\mathsf{I_{\overline{y}\overline{z}}=0}\) \(\mathsf{I_{yz} = 0}\)