Analytical#
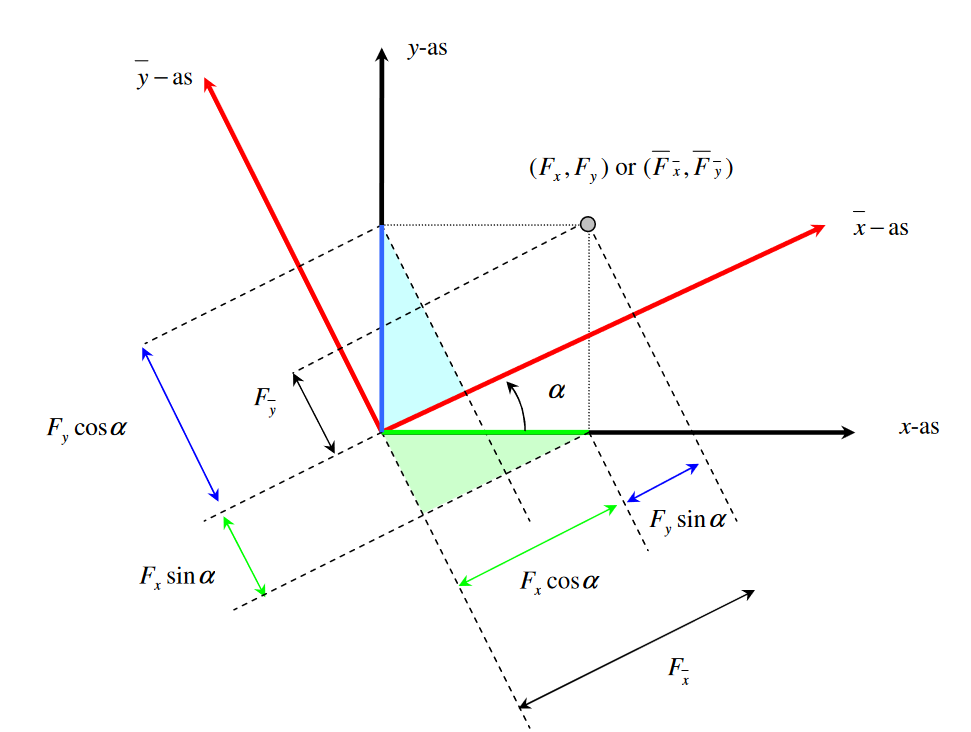
Transformations#
The rotation matrix R is defined as:
Rotating a first-order tensor (for example force \(F\)) by an angle \(\alpha\) is defined as:
The transformation rule for a second order tensor (for example stiffness matrix \(K\)) is defined in matrix notation as:
This is treated in chapter 2.1 of the lecture notes Introduction to Continuum Mechanics (Hartsuijker and Welleman, 2007).
The individual terms of \(\bar{\mathrm{K}}\) can be written out as:
\(k_{\bar x \bar x} = \cfrac{1}{2}\left(k_{xx} + k_{yy}\right) + \cfrac{1}{2}\left(k_{xx} - k_{yy}\right) \cos \left(2\alpha\right) + k_{xy} \sin \left(2 \alpha\right)\)
\(k_{\bar y \bar y} = \cfrac{1}{2}\left(k_{xx} + k_{yy}\right) - \cfrac{1}{2}\left(k_{xx} - k_{yy}\right) \cos \left(2\alpha\right) - k_{xy} \sin \left(2 \alpha\right)\)
\(k_{\bar x \bar y} = -\cfrac{1}{2}\left(k_{xx} - k_{yy}\right) \sin \left(2 \alpha \right) + k_{xy} \cos \left(2 \alpha\right)\)
The principal values of the second order tensor \(\bar{\mathrm{K}}\) are defined by:
The principal directions of the second order tensor \(\bar{\mathrm{K}}\) are defined by:
This is treated in chapter 2.3 of the lecture notes Introduction to Continuum Mechanics (Hartsuijker and Welleman, 2007).
