Core of a cross-section

Core of a cross-section#

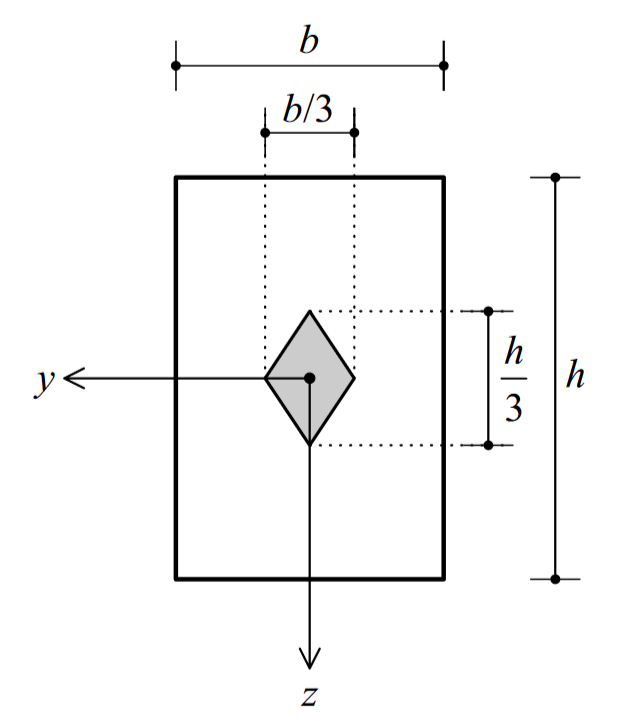
../../_images/image8.png

Fig. 36 Figure 9.80 Hartsuijker and Welleman (2007)#

Core of cross-section#

A centre of force within the core corresponds with a stress distribution in the cross-section that does not exhibit a change in sign.

This is treated in chapter 4.9 and 9.15.1 of the book Engineering Mechanics Volume 2 (Hartsuijker and Welleman, 2007). Chapter 9 is not part of the Dutch version but can be found chapter 1.5 of Niet-symmetrische en inhomogene doorsnedes (Hartsuijker and Welleman, 2009).

To find the complete core of a cross-section the method is treated for nonsymmetrical cross-sections in chapter 9.15.2 of the book Engineering Mechanics Volume 2 (Hartsuijker and Welleman, 2007). For symmetrical cross-sections the following relations simplify:

  • Equation 9.40 transforms into two independent equations: \(M_y = EI_{yy} \cdot \kappa_y\) and \(M_z = EI_{zz} \cdot \kappa_z\)

  • Equation 9.75 transforms into two independent equations: \(e_y = -\cfrac{I_{yy}}{A \cdot y_1}\) and \(e_z = -\cfrac{I_{zz}}{A \cdot z_1}\)

Example complete core of a symmetrical cross-section#

Give is the following cross-section:

../../_images/cross-section.svg

with:

  • \(A = 180000 \text{ mm}^2\)

  • \(I_{zz} = 4.134375 \cdot 10^9 \text{ mm}^4\)

  • \(I_{yy} = 2.3625 \cdot 10^9 \text{ mm}^4\)

The core is defined by the neutral axes along the sides of the cross-section: side \(\text{AI}\), \(\text{IH}\), \(\text{EH}\), \(\text{DE}\) and symmetrical \(\text{BD}\) and \(\text{AB}\).

Side \(\text{AI}\)#

For \(\text{AI}\), \(y_1 = \infty\) and \(z_1 = -225 \text{ mm}\):

../../_images/z1.svg

This results in:

  • \(e_y = -\cfrac{2.3625 \cdot 10^9 }{180000 \cdot \infty} = 0 \text{ mm}\)

  • \(e_z = -\cfrac{4.134375 \cdot 10^9}{180000 \cdot -225} \approx 102 \text{ mm} \)

This gives the first core point:

../../_images/e1.svg

Side \(\text{IH}\)#

For \(\text{IH}\), \(y_1 = -225 \text{ mm}\) and \(z_1 = \infty\). This results in:

  • \(e_y = -\cfrac{2.3625 \cdot 10^9 }{180000 \cdot -225} \approx 58 \text{ mm}\)

  • \(e_z = -\cfrac{4.134375 \cdot 10^9}{180000 \cdot \infty} = 0 \text{ mm}\)

Side \(\text{EH}\)#

For \(\text{EH}\), \(y_1\) and \(z_1\) can not directly be found from the figure, but need to be calculated. The points \(\text{E } \left(-75,375\right)\) and \(\text{H }\left(-225,75\right)\) are known, giving the equation for the neutral axis: \(z = 2 \cdot y + 525\). This gives \(y_1 = -262.5 \text{ mm}\) and \(z_1 = 525 \text{ mm}\).

../../_images/z2.svg

This results in:

  • \(e_y = -\cfrac{2.3625 \cdot 10^9 }{180000 \cdot -262.5} = 50\text{ mm}\)

  • \(e_z = -\cfrac{4.134375 \cdot 10^9}{180000 \cdot 525} = -43.75 \text{ mm} \)

Side \(\text{DE}\)#

For \(\text{IH}\), \(y_1 = \infty\) and \(z_1 = 375 \text{ mm}\). This results in:

  • \(e_y = -\cfrac{2.3625 \cdot 10^9 }{180000 \cdot \infty} = 0 \text{ mm}\)

  • \(e_z = -\cfrac{4.134375 \cdot 10^9}{180000 \cdot 375} = -61.25 \text{ mm}\)

Side \(\text{DB}\)#

Side \(\text{DB}\) is the mirror neutral axis and core point from \(\text{EH}\) giving:

  • \(e_y = -50 \text{ mm}\)

  • \(e_z = -43.75 \text{ mm} \)

Side \(\text{AB}\)#

Side \(\text{AB}\) is the mirror neutral axis and core point from \(\text{HI}\) giving:

  • \(e_y \approx -58 \text{ mm}\)

  • \(e_z = 0 \text{ mm} \)

Core#

All these points result in the core:

../../_images/core.svg

Exercises#

Contents