Macaulays methode

Macaulays methode is een methode waarmee de verplaatsingsfunctie van een ligger van meerdere segmenten kan worden bepaald in één functie (Macaulay, 1919). Daarbij is het niet nodig om een balk onder te verdelen in segmenten met randvoorwaarden (afhankelijk van verdeelde belastingen, puntlasten, opleggingen, etc.) en blijft de notatie direct herkenbaar bij integratie/differentiatie (in tegenstelling tot de Dirac delta / Heaviside functies). Er bestaat een implementatie voor deze methode voor balken, maar een uitbreiding naar 2d-constructies zoals portalen ontbreekt.

Voorbeeld Macaulays methode zonder uitbreidingen

Laten we de volgende constructie bekijken:

Fig. 1 Voorbeeld constructie

Definieer belasting

Deze belasting (inclusief oplegreacties) kan als volgt worden beschreven volgens Macaulay:

\[q\left( x \right)=\underbrace{{{A}_{v}}{{\left\langle x \right\rangle }^{-1}}+{{B}_{v}}{{\left\langle x-15 \right\rangle }^{-1}}}_{\text{oplegreacties}}\underbrace{+10{{\left\langle x \right\rangle }^{0}}-10{{\left\langle x-4 \right\rangle }^{0}}}_{\text{verdeelde belasting}}\underbrace{+35{{\left\langle x-9 \right\rangle }^{-1}}}_{\text{puntlast}}\]

Dit kan in sympy worden genoteerd als:

import sympy as sym
sym.init_printing()

x = sym.symbols('x')
EI = sym.symbols('EI')
C_1, C_2, C_3, C_4 = sym.symbols('C_1 C_2 C_3 C_4') 
A_v, B_v = sym.symbols('A_v B_v')

Q = 10
L = 15
a = 4
b = 5
F = 35

q =  A_v * sym.SingularityFunction(x,0,-1) + Q * sym.SingularityFunction(x,0,0) - Q * sym.SingularityFunction(x,a,0) + F * sym.SingularityFunction(x, a+b, -1) + B_v * sym.SingularityFunction(x,L,-1)
display(q)

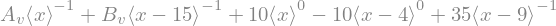
Definieer randvoorwaarden

Voor dit probleem gelden de volgende randvoorwaarden:

\[\begin{split}\begin{align} & w\left( 0 \right)=0 \\ & w\left( 15 \right)=0 \\ & M\left( 0 \right)=0 \\ & M\left( 15 \right)=0 \\ & V\left( {{0}^{-}} \right)=0 \\ & V\left( {{15}^{+}} \right)=0 \\ \end{align}\end{split}\]

Dit kan in sympy als volgt worden gedefinieerd:

V = -sym.integrate(q, x) + C_1
M = sym.integrate(V, x) + C_2
kappa = M / EI
phi = sym.integrate(kappa, x) + C_3
w = -sym.integrate(phi, x) + C_4
display(w)

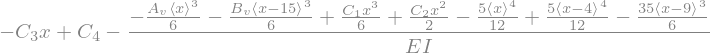
De dwarskracht net links van \(0\) en net rechts van \(15\) wordt gemodelleerd met een ‘dummy’-variabele van \(\cfrac{1}{\infty}\).

oo = sym.Dummy('oo', prime=True)
very_small = 1/oo

Nu kunnen in SymPy de vergelijkingen voor de randvoorwaarden worden opgesteld:

Eq1 = sym.Eq(w.subs(x,0),0)
Eq2 = sym.Eq(w.subs(x,L),0)
Eq3 = sym.Eq(M.subs(x,0),0)
Eq4 = sym.Eq(M.subs(x,L),0)
Eq5 = sym.Eq(V.subs(x,0-very_small),0).subs(oo,sym.oo)
Eq6 = sym.Eq(V.subs(x,L+very_small),0).subs(oo,sym.oo)
display(Eq1, Eq2, Eq3, Eq4, Eq5, Eq6)

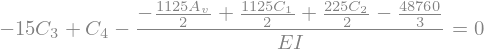
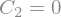
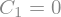
Los op voor randvoorwaarden

Oplossen naar de randvoorwaarden geeft:

\[w\left( x \right)=\frac{26692x\underbrace{-292{{\left\langle x \right\rangle }^{3}}-158{{\left\langle x-15 \right\rangle }^{3}}}_{\text{oplegreacties}}\underbrace{+15{{\left\langle x \right\rangle }^{4}}-15{{\left\langle x-4 \right\rangle }^{4}}}_{\text{verdeelde belasting}}\underbrace{+210{{\left\langle x-9 \right\rangle }^{3}}}_{\text{puntlast}}}{36EI}\]

welke oplossing ook met code kan worden gevonden:

sol = sym.solve((Eq1,Eq2,Eq3,Eq4,Eq5,Eq6),(C_1,C_2,C_3,C_4,A_v,B_v))
display(sol)

display(w.subs(sol).factor(EI))

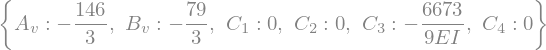
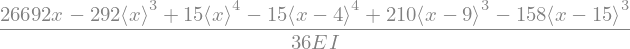
Dit kan ook worden omgeschreven naar een functie per domein:

\(\displaystyle \begin{cases} \frac{79 x^{3} - 3555 x^{2} + 40781 x - 78465}{18 EI} & \text{for}\: x > 9 \\\frac{- 13 x^{3} - 360 x^{2} + 7633 x - 960}{9 EI} & \text{for}\: x > 4 \\\frac{x \left(15 x^{3} - 292 x^{2} + 26692\right)}{36 EI} & \text{for}\: x > 0\end{cases}\)

wat met de volgende code kan worden gevonden:

display(sym.simplify(w.subs(sol).rewrite(sym.Piecewise)))

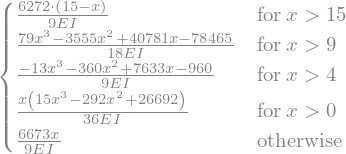
Dit resultaat kan ook worden geplot voor een \(EI\) van \(10000\):

import numpy as np
import matplotlib.pyplot as plt

%config InlineBackend.figure_formats = ['svg']

w_numpy = sym.lambdify(x, w.subs(sol).subs(EI,10000).rewrite(sym.Piecewise))

x_numpy = np.linspace(0,15,100)
plt.figure()
plt.plot(x_numpy,w_numpy(x_numpy))
plt.xlabel('$x$')
plt.ylabel('$w$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()

The dwarskrachtverdeling kan ook worden gevonden:

\[V\left( x \right)=\underbrace{\frac{146{{\left\langle x \right\rangle }^{0}}}{3}+\frac{79{{\left\langle x-15 \right\rangle }^{0}}}{3}}_{\text{oplegreacties}}\underbrace{-10{{\left\langle x \right\rangle }^{1}}+10{{\left\langle x-4 \right\rangle }^{1}}}_{\text{verdeelde belasting}}\underbrace{-35{{\left\langle x-9 \right\rangle }^{0}}}_{\text{puntlast}}\]

met de volgende code:

display(V.subs(sol))

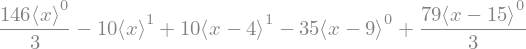
En ook deze formule kan worden omgeschreven naar een formule per domein:

\[\begin{split}\displaystyle \begin{cases} - \frac{79}{3} & \text{for}\: x > 9 \\\frac{26}{3} & \text{for}\: x > 4 \\\frac{146}{3} - 10 x & \text{for}\: x > 0 \end{cases}\end{split}\]

display(sym.simplify(V.subs(sol).rewrite(sym.Piecewise)))

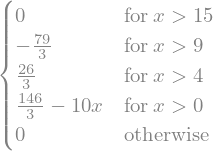
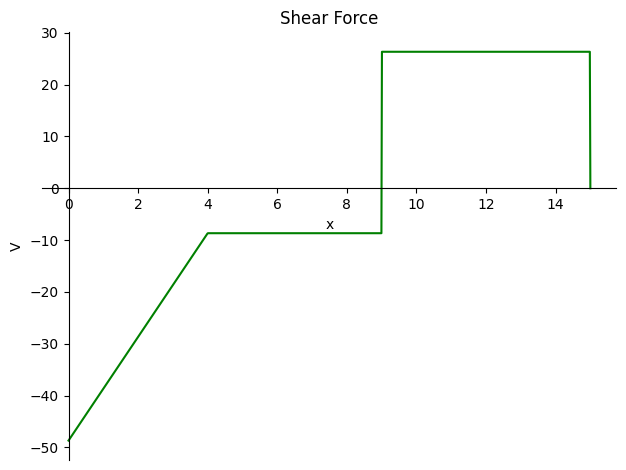
en kan ook worden geplot:

V_numpy = sym.lambdify(x, V.subs(sol).rewrite(sym.Piecewise))

x_numpy = np.linspace(0,15.01,10000)
plt.figure()
plt.plot(x_numpy,V_numpy(x_numpy))
plt.xlabel('$x$')
plt.ylabel('$V$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()

Voorbeeld Macaulays methode in SymPy

De methode van Macaulay is ook geïmplementeerd in SymPy en kan daar worden toegepast zonder vergelijkingen op te moeten stellen.

Let op: het assenstelsel is in SymPy gedefinieerd met de verticale as positief naar boven.

import sympy as sym
from sympy.physics.continuum_mechanics.beam import Beam
sym.init_printing()

E, I = sym.symbols('E, I')
b = Beam(15, E, I)
A_v = b.apply_support(0,type='pin')
B_v = b.apply_support(15,type='roller')
b.apply_load(-10, 0, 0, 4)
b.apply_load(-35, 9, -1)
b.solve_for_reaction_loads(A_v, B_v)
b.deflection().simplify()

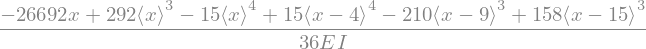
b.plot_deflection({E : 10000, I : 1});

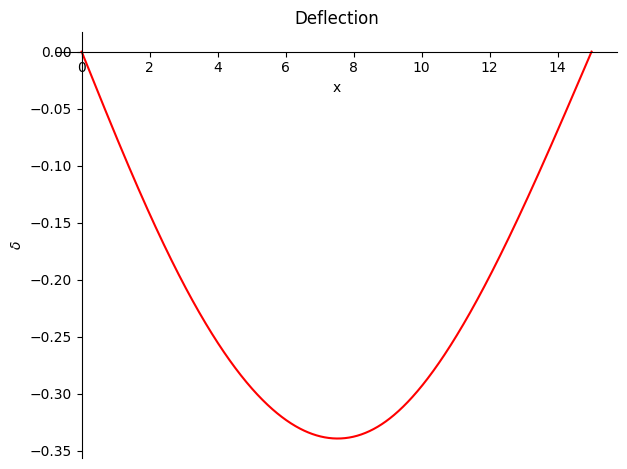
b.plot_shear_force();