Huidige uitbreidingen

Dit rapport zal een overzicht bevatten van de opgedane kennis met betrekking tot de methode van Macaulay. Dit rapport is bedoeld voor personen met mechanica kennis die nog onbekend zijn met de methode van Macaulay. In dit rapport zal de methode van Macaulay worden toegelicht en zal er worden aangegeven hoe deze toegepast kan worden.

Dit rapport bestaat uit 4 hoofdstukken:

1. De methode van Macaulay

2. Modelleren van krachten, opleggingen en verbindingen

3. Invloedslijnen met Macaulay

4. Oplossen van 2D constructies

In dit rapport wordt er gerefereerd naar de werken van van der Wulp (2023), Jankie (2023), Baudoin (2024) en van Gelder (2024) en wordt er hevig gebruik gemaakt van citaties en parafraseringen.

De methode van Macaulay

Belastingvergelijking

Uit de balkentheorie van Euler-Bernoulli kunnen de differentiaalvergelijkingen voor buiging (1) en extensie (2) worden afgeleid. Begrip over de afleiding en het gebruik van deze vergelijkingen wordt als voorkennis beschouwd.

(1)\[EI\frac{d^{4}w}{dx^{4}} - q_{z}\left( x \right) = 0\]

(2)\[EA\frac{d^{2}w}{dx^{2}} + q_{x}\left( x \right) = 0\]

Over het algemeen worden deze vergelijkingen gebruikt door liggers eerst in verschillende delen met gelijke belasting op te splitsen. Vervolgens kan ieder deel beschreven worden met de differentiaalvergelijking en wordt er gebruik gemaakt van overgangsvoorwaarden.

Bij de methode van Macaulay wordt er op een andere manier gebruik gemaakt van deze differentiaalvergelijkingen. De methode van Macaulay maakt gebruik van singulariteitsfuncties om de belasting op een ligger te beschrijven. Dit heeft als grote voordeel dat een ligger niet opgesplitst hoeft te worden in verschillende delen. Het gedrag van een ligger kan zo in één vergelijking worden beschreven.

Singulariteitsfuncties

Zoals hierboven aangegeven maakt de methode van Macaulay gebruik van singulariteitsfuncties. Dit is een familie van functies die gebaseerd is op de Dirac-delta functie. Het differentiëren en integreren van deze Dirac-delta functie vormt deze familie. De singulariteitsfunctie is wiskundig als volgt gedefinieerd:

Voor \(n\ \geq \ 0\):

(3)\[\begin{split}f\left( x \right) \equiv {\left\langle {x - \bar x} \right\rangle ^n} = \left\{ \begin{array}{l} {\left( {x - \bar x} \right)^n} & x \ge \bar x \\ 0 & x < \bar x \end{array} \right.\end{split}\]

Voor \(n < \ 0\):

(4)\[f\left( x \right) \equiv {\left\langle {x - \bar x} \right\rangle ^n} = 0\]

Hierin geeft \(\bar x\) de positie aan waar de singulariteit voorkomt, en is \(n\) de orde van de functie.

Hierbij is (4) aangepast waarbij er origineel op \(x=\bar x\) geldt \(f\left(x\right)=\infty\). Dit heeft echter geen betekening voor het balkmodel.

Het integreren van de singulariteitsfunctie is afhankelijk van zijn orde en is als volgt gedefinieerd:

(5)\[\begin{split}\int {{{\left\langle {x - \bar x} \right\rangle }^n}{\rm{d}}x} = \left\{ \begin{array}{l} {\left( {x - \bar x} \right)^{n + 1}} & n < 0\\ \cfrac{{{{\left( {x - \bar x} \right)}^{n + 1}}}}{{n + 1}} & n \ge 0 \end{array} \right.\end{split}\]

Een aantal voorbeelden zijn hieronder weergegeven

Voorbeeld \(n = -1\)

Voor \(n = -1\) evalueert de functie (4) voor het gehele domein naar 0. Als de originele definitie wordt aangehouden met \(f\left(\bar x\right)=\infty\) staat deze functie ook wel bekend als de Dirac-Delta functie.

Voorbeeld \(n = 0\)

Voor \(n=0\) evalueert de functie (4) tot een stapfunctie, ook wel bekend als de Heaviside.

Fig. 2 Plot of \(\left\langle {x - \bar x} \right\rangle ^0\)

Voorbeeld \(n = 1\)

Voor \(n=1\) geeft de functie (4) een linear verband na \(\bar x\).

Fig. 3 Plot of \(\left\langle {x - \bar x} \right\rangle ^1\)

Oplossingsstrategie

De eerste stap bij het oplossen van een probleem met de methode van Macaulay is het opstellen van de belastingvergelijking in de langs- en loodrechte richting. Hiervoor wordt de hele constructie gemodelleerd in één vergelijking per richting. Deze vergelijking kan vervolgens ingevuld worden als \(q\) in de differentiaalvergelijkingen in ref(hoofdstuk_1_1). Hoe verschillende onderdelen van een constructie gemodelleerd kunnen worden in deze vergelijking is beschreven in ref(hoofdstuk_2).

Als de belastingvergelijking is gevonden kan deze geïntegreerd worden. Dit geeft vergelijkingen die de normaalkrachten, dwarskracht, het moment, de rotatie, de doorbuiging en extensie van de staaf beschrijven. In deze vergelijkingen staan nog onbekende reactiekrachten en integratieconstanten.

Om deze onbekende reactiekrachten en integratieconstanten op te lossen kunnen de randvoorwaarden worden opgesteld. Met deze randvoorwaarden kunnen de onbekende waardes worden gevonden.

De gevonden waardes voor de reactiekrachten en integratieconstanten kunnen worden ingevuld in de vergelijkingen. Dit geeft de vergelijkingen die het gedrag van de staaf beschrijven.

Modelleren van belastingen, opleggingen en verbindingen

Assenstelsel

Het model maakt gebruik van een globaal en een lokaal assenstelsel. Het globale assenstelsel bestaat uit een horizontale en een verticale as waarbij de positieve richtingen naar rechts en naar beneden wijzen. Het lokale assenstelsel bestaat uit een \(x\)-as en een \(z\)-as. De positieve \(x\)-as wordt afgebeeld met een blauwe pijl zichtbaar in Fig. 4en de positieve \(z\)-as is altijd een kwartslag met de klok mee t.o.v. de positieve \(x\)-as.

Alle belastingen werken langs de globale assen, verdeelde belastingen werken langs de lengte van de staaf (zoals eigengewicht) en hoeken worden gemeten van de positieve \(v\)-as naar de positieve \(h\)-as

De externe krachten en de verplaatsingen worden globaal genoteerd en de snedekracht-diagrammen lokaal. Er zijn twee vergelijkingen die de lokale as volgen. \(q_{z}(x)\) is voor de krachten loodrecht op de staaf en integreert naar de dwarskrachtenvergelijking, enz. en \(q_{x}(x)\) is voor de krachten parallel aan de staaf en integreert naar de normaalkrachtenvergelijking, enz.

Voor een constructie in 1D komen de lokale en globale assen overeen en hebben alle staven dezelfde oriëntatie.

Fig. 4 Positieve assen in 2D constructie (Baudoin, 2024)

Modelleren van belastingen

Voor het modelleren van belastingen op de constructie wordt gebruik gemaakt van singulariteitsfuncties. Dit maakt het mogelijk om de volledige constructie in één regel (per richting) te beschrijven en daarmee de differentiaalvergelijking op te lossen. Er zal nu toegelicht worden hoe verschillende krachten beschreven kunnen worden met singulariteitsfuncties.

Belastingen kunnen worden beschreven door de een singulariteitsfunctie van bijbehorende orde te vermenigvuldigen met de waarde van de kracht of verbinding. Naar aanleiding van het assenstelsel wordt een kracht positief of negatief gemodelleerd.

Puntlast

Een puntlast geeft belasting op een enkele plek in de constructie. Een puntlast kan gemodelleerd worden met de Dirac-delta functie. Een puntlast met een waarde \(F\), ter plaatse van punt \(\bar x\) waarbij de staaf een hoek \(\theta \left( \bar x \right)\) heeft, wordt gemodelleerd zoals getoond in (6) en (7).

(6)\[\begin{align} &{{q_z\left(x\right) : F \left\langle x - \bar x \right\rangle^{- 1}}} &{{q_x\left(x\right) : F \left\langle x - \bar x \right\rangle^{- 1}}} \end{align}\]

In 2d wordt de kracht ontbonden in de langs- en loodrechte richting:

(7)\[\begin{split}\begin{align} &q_z\left(x\right) : &F_{v} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left(\bar x\right) \right) &+F_{h} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left(\bar x\right) \right) \\ &q_x\left(x\right) : &- F_{v} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta\left(\bar x\right) \right) &+F_{h} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left(\bar x\right) \right) \end{align}\end{split}\]

Koppel

Een koppel werkt ook op een enkel punt in de constructie. Een koppel wordt beschreven door de orde \(-2\) in de krachtenvergelijking van de loodrechte richting aangezien dit koppel geen invloed heeft op de langsrichting. Een koppel met waarde \(T\) ter plaatse van punt \(\bar x\) waarbij de staaf een hoek \(\theta \left( \bar x \right)\) heeft, wordt als volgt gemodelleerd in 1D en 2D:

(8)\[q_z\left(x\right) : T \left\langle x - \bar x \right\rangle^{- 2}\]

(9)\[\begin{split}\begin{align} &q_z\left(x\right): &T \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right): &0 \end{align}\end{split}\]

Uniform verdeelde belasting

Belasting die gelijkmatig verdeeld is over de constructie kan beschreven worden met twee Heaviside functies. Hierbij werkt de waarde van \(q_{z}\) eerste vanaf \(\bar x_1\) in de daadwerkelijke richtingen en dan vanaf \(\bar x_2\) in tegengestelde richting, dit geeft een totaal van \(0\) voor \(x > \bar x_2\). Deze werking is in Fig. 5 weergegeven.

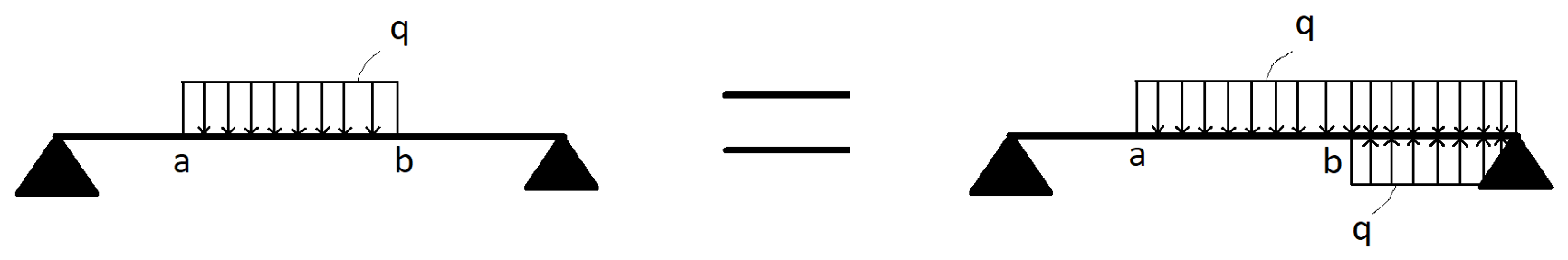
Fig. 5 Modelleren van een uniform verdeelde belasting (van der Wulp, 2023)

Dit kan beschreven worden met singulariteitsfuncties met groottes \(q_v\) en \(q_h\) van punt \(\bar x_1\) tot \(x_2\) waarbij de staaf een hoek \(\theta \left( \bar x_1 \right)\) en \(\theta \left( \bar x_2 \right)\) heeft in 1D en 2D:

(10)\[\begin{split}\begin{align} &q_z\left(x\right): &q_v \left\langle x - \bar x_1 \right\rangle^{- 1} &-q_v\left\langle x - \bar x_2 \right\rangle^{- 1} \\ &q_z\left(x\right): &q_h \left\langle x - \bar x_1 \right\rangle^{- 1} &-q_h\left\langle x - \bar x_2 \right\rangle^{- 1} \end{align}\end{split}\]

(11)\[\begin{split}\begin{align} &q_z\left(x\right): &q_{v} \left\langle x - \bar x_1 \right\rangle^{- 1} \cos \left( \theta \left(\bar x_1\right) \right) &-q_{v} \left\langle x_2 - \bar x \right\rangle^{- 1} \cos \left( \theta \left(\bar x_2\right) \right) \\ & &+ q_{h} \left\langle x - \bar x_1 \right\rangle^{- 1} \sin \left( \theta \left(\bar x_1\right) \right) &-q_{h} \left\langle x - \bar x_2 \right\rangle^{- 1} \sin \left( \theta \left(\bar x_2\right) \right) \\ & q_x \left(x \right) : &- q_{v} \left\langle x - \bar x_1 \right\rangle^{- 1} \sin \left( \theta \left(\bar x_1\right) \right) &+q_{v} \left\langle x - \bar x_2 \right\rangle^{- 1} \sin \left( \theta \left(\bar x_2\right) \right) \\ &&+q_{h} \left\langle x - \bar x_1 \right\rangle^{- 1} \cos \left( \theta \left(\bar x_1\right) \right) &- q_{h} \left\langle x - \bar x_2 \right\rangle^{- 1} \cos \left( \theta \left(\bar x_2\right) \right) \end{align}\end{split}\]

Lineair en parabolisch verdeelde belastingen

Belastingen die niet uniform maar lineair of parabolisch verdeeld zijn kunnen op eenzelfde manier gemodelleerd worden als de uniform verdeelde belasting.

Modelleren van opleggingen en verbindingen

Naast belastingen kunnen ook opleggingen en verbindingen worden gemodelleerd door middel van singulariteitsfuncties. Op de plek waar een oplegging of verbinding wordt toegevoegd gelden ook randvoorwaarden. Deze randvoorwaarden worden gebruikt om de vergelijkingen uiteindelijk op te lossen. Er zal nu worden toegelicht hoe verschillende opleggingen en verbindingen kunnen worden beschreven door middel van singulariteitsfuncties en welke randvoorwaarden daarbij horen. Er wordt in dit hoofdstuk alleen gekeken naar krachten loodrecht op de staaf en momenten. Krachten evenwijdig aan de staaf worden behandeld in het ref(hoofdstuk_2.3)Modelleren van opleggingen en verbindingen voor extensie.

Inklemming

Bij een inklemming kunnen een verticale oplegreactie en een inklemmingsmoment optreden. In Fig. 6 is weergegeven hoe een inklemming gemodelleerd kan worden.

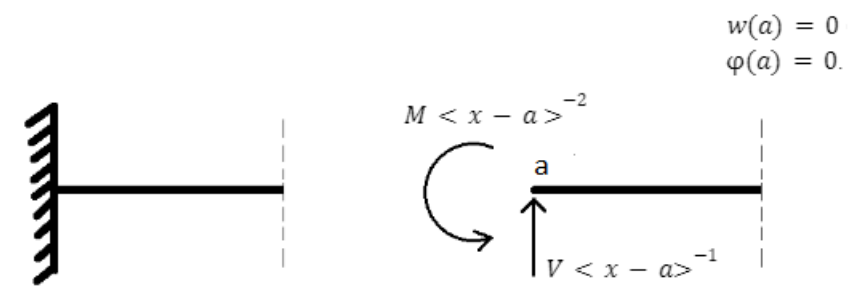
Fig. 6 Modelleren van een inklemming (van der Wulp, 2023)

Dit kan beschreven worden met singulariteitsfuncties met ordes \(-1\) en \(-2\) met onbekende groottes \(R_v\), \(R_h\) en \(T\) op punt \(\bar x\) waarbij de staaf een hoek \(\theta \left( \bar x \right)\) heeft in 1D en 2D:

(12)\[\begin{split}\begin{align} &q_z\left(x\right) : &R_{v} \left\langle x - \bar x \right\rangle^{- 1} &+ T \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right) : &R_{h} \left\langle x - \bar x \right\rangle^{- 1} \end{align}\end{split}\]

(13)\[\begin{split}\begin{align} &q_z\left(x\right) : &R_{h} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x \right) \right) &+ R_{v} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left( \bar x \right) \right) &+ T \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right) : &R_{h} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left( \bar x \right) \right) &- R_{v} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x \right) \right) \end{align}\end{split}\]

Daarnaast introduceert een inklemming ook drie randvoorwaarden:

(14)\[\begin{split}\begin{align} &\varphi \left( \bar x \right) = 0\\ &u_v \left(\bar x\right) = 0\\ &u_h \left(\bar x\right) = 0 \end{align}\end{split}\]

Scharnier- en roloplegging

Aangezien krachten in de richting van de staaf nog niet worden meegenomen, kunnen scharnier- en rolopleggingen op dezelfde manier worden gemodelleerd. In Fig. 7 en Fig. 8 is weergegeven hoe een scharnieroplegging gemodelleerd kan worden.

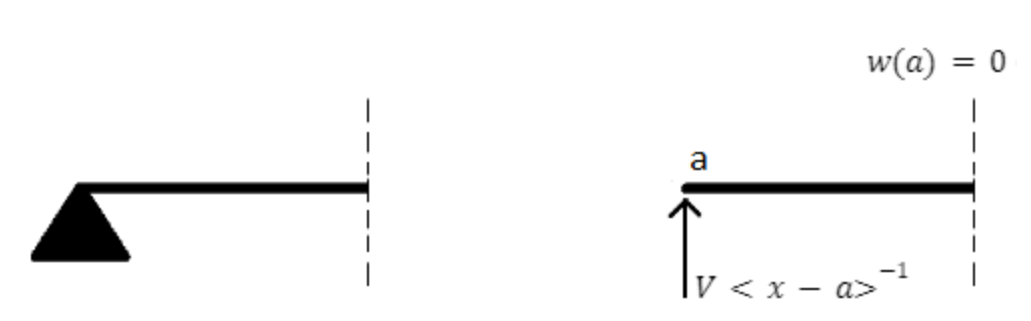
Fig. 7 Modelleren van en scharnieroplegging (van der Wulp, 2023)

Fig. 8 Modelleren van een scharnieroplegging bij extensie (van der Wulp, 2023)

Dit kan beschreven worden met singulariteitsfuncties met ordes \(-1\) met onbekende groottes \(R_v\), \(R_h\) en \(T\) op punt \(\bar x\) waarbij de staaf een hoek \(\theta \left( \bar x \right)\) heeft in 1D en 2D:

(15)\[\begin{split}\begin{align} &q_z\left(x\right) : &R_{v} \left\langle x - \bar x \right\rangle^{- 1} \\ &q_x\left(x\right) : &R_{h} \left\langle x - \bar x \right\rangle^{- 1} \end{align}\end{split}\]

(16)\[\begin{split}\begin{align} &q_z\left(x\right) : &R_{h} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x \right) \right) &+ R_{v} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left( \bar x \right) \right) \\ &q_x\left(x\right): &R_{h} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left( \bar x \right) \right) &- R_{v} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x \right) \right) \end{align}\end{split}\]

Daarnaast introduceert een scharnier ook twee randvoorwaarden:

(17)\[\begin{split}\begin{align} &u_v \left(\bar x\right) = 0\\ &u_h \left(\bar x\right) = 0 \end{align}\end{split}\]

Bij een rolscharnier vervallen de krachten en vergelijkingen in vrijgemaakte richting

Scharnier

Scharnierende verbindingen in constructies kunnen worden beschreven met singulariteitsfuncties van orde \(-3\). Dit valt te beredeneren uit het feit dat scharnieren een sprong in de krommingslijn geven, en daar dus orde \(0\) hebben. Terug differentiëren naar de belasting vergelijking geeft een singulariteitsfunctie van orde \(-3\).

In Fig. 9 is weergegeven hoe een scharnier gemodelleerd kan worden.

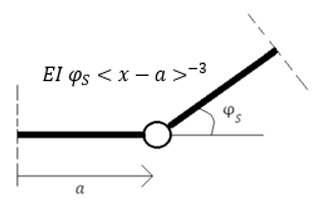
Fig. 9 Modelleren van een scharnier (van der Wulp, 2023), correctie (van Gelder, 2024)

Dit kan beschreven worden met singulariteitsfuncties met orde \(-3\) met onbekende grootte \(\Delta \varphi\) op punt \(\bar x\) in zowel 1D als 2D met dezelfde vergelijking:

(18)\[q_z\left(x\right) : EI \ \Delta \varphi \left\langle x - \bar x \right\rangle^{- 3}\]

Een scharnier introduceert ook een randvoorwaarde. Ter plaatse van het scharnier is het moment (\(M\)) gelijk aan \(0\).

(19)\[M \left(\bar x\right) = 0\]

Schuifscharnier

Schuifscharnieren in een constructie kunnen worden beschreven met singulariteitsfuncties van orde \(-4\). Zoals roterende scharnieren een sprong geven in de krommingslijn, geven schuifscharnieren een sprong in de doorbuigingslijn. Hieruit volgt dat schuifscharnieren in de belasting vergelijking beschreven worden met een singulariteitsfunctie van orde \(-4\).

In Fig. 10 is weergegeven hoe een schuifscharnier gemodelleerd kan worden.

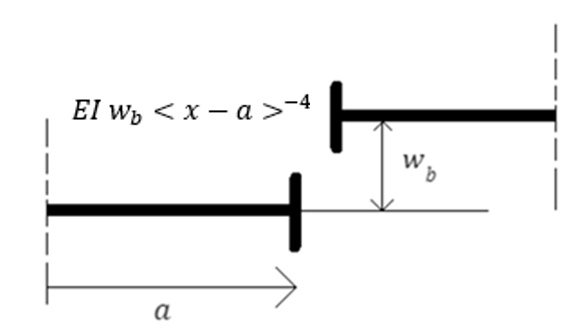
Fig. 10 Modelleren van een scharnier (van der Wulp, 2023), correctie (van Gelder, 2024)

Dit kan beschreven worden met singulariteitsfuncties met ordes \(-4\) met onbekende grootte \(\Delta u_z\) op punt \(\bar x\):

(20)\[q_z\left(x\right) : EI \ \Delta u_z \left\langle x - \bar x \right\rangle^{- 4}\]

Een schuifscharnier introduceert ook een randvoorwaarde. Ter plaatse van het schuifscharnier is de dwarskracht (\(V\)) gelijk aan \(0\).

(21)\[V \left(\bar x\right) = 0\]

Telescoopscharnieren

Deze scharnieren hebben axiale verplaatsing als vrijheidsgraad. Dit geeft een sprong in de vergelijking voor axiale verplaatsing ter plaatse van het scharnier. Deze spong kan gemodelleerd worden met de Heaviside functie. Terug differentiëren naar de belastingvergelijking geeft dan een singulariteitsfunctie met orde \(-2\).

In Fig. 11 is weergegeven hoe een telescoopscharnier gemodelleerd kan worden.

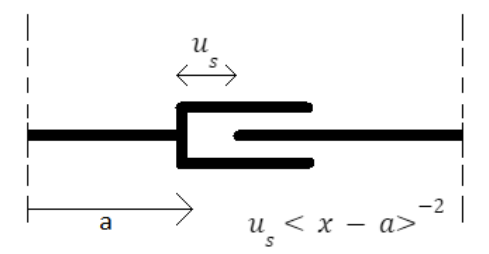
Fig. 11 Modelleren van telescoop scharnieren (van der Wulp, 2023)

Dit kan beschreven worden met singulariteitsfuncties met ordes \(-2\) met onbekende grootte \(\Delta u_x\) op punt \(\bar x\):

(22)\[q_x\left(x\right) : EA \ \Delta u_x \left\langle x - \bar x \right\rangle^{- 2}\]

Een telescoopscharnier introduceert ook een randvoorwaarde. Ter plaatse van het telescoopscharnier is de normaalkracht (\(N\)) gelijk aan \(0\).

(23)\[N \left(\bar x\right) = 0\]

Verende opleggingen

Er zijn twee soorten verende opleggingen: verende opleggingen die verplaatsing tegengaan en verende opleggingen die rotatie tegen gaan. In beide gevallen wordt de veer gemodelleerd als kracht ter plaatse van de oplegging in de belasting vergelijking.

In Fig. 12, Fig. 13 en Fig. 14 is weergegeven hoe de veren gemodelleerd kunnen worden.

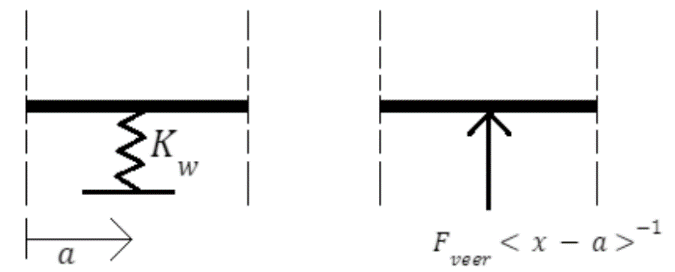
Fig. 12 Modelleren van een translerende verende oplegging (van der Wulp, 2023)

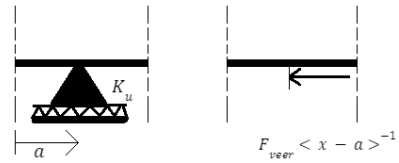
Fig. 13 Modelleren van een verende scharnieroplegging bij extensie (van der Wulp, 2023)

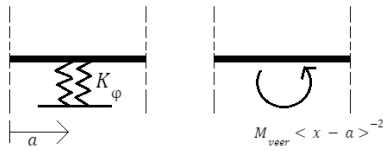
Fig. 14 Modelleren van een roterende verende oplegging (van der Wulp, 2023)

Een verende oplegging in alle richtingen die verticale verplaatsing tegengaat wordt gemodelleerd als puntlast met een grootte van \(F_{\text{veer},v}\), \(F_{\text{veer},h}\), \(T_{\text{veer}}\).

Dit kan beschreven worden met singulariteitsfuncties met ordes \(-1\) en \(-2\) met onbekende groottes \(R_v\), \(R_h\) en \(T\) op punt \(\bar x\) waarbij de staaf een hoek \(\theta \left( \bar x \right)\) heeft in 1D en 2D:

(24)\[\begin{split}\begin{align} &q_z\left(x\right) : &F_{\text{veer},v} \left\langle x - \bar x \right\rangle^{- 1} &+ T_{\text{veer}} \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right) : &F_{\text{veer},h} \left\langle x - \bar x \right\rangle^{- 1} \end{align}\end{split}\]

(25)\[\begin{split}\begin{align} &q_z\left(x\right) : &F_{\text{veer},h} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x \right) \right) &+ F_{\text{veer},v} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left( \bar x \right) \right) &+ T_{\text{veer}} \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right) : &R_{\text{veer},h} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left( \bar x \right) \right) &- R_{\text{veer},v} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x \right) \right) \end{align}\end{split}\]

De randvoorwaardes die hierbij worden geintroduceerd zijn bevatten de veerconstantes \(K_T\), \(K_V\) en \(K_N\):

(26)\[\begin{split}\begin{align} & T_{\text{veer}} = - {K_M} \varphi \ \left( \bar x \right) \\ & F_{\text{veer},v} = - {K_V} \ u_v \left(\bar x\right)\\ & F_{\text{veer},h} = - {K_N} \ u_h \left(\bar x\right) \end{align}\end{split}\]

Een deels verende oplegging is natuurlijk ook mogelijk met het weglaten van de desbetreffende termen.

Verende verbindingen

Verende verbindingen worden gemodelleerd als de verbinding waar het om gaat met een andere randvoorwaarde.

In Fig. 15, Fig. 16 en Fig. 17 is weergegeven hoe de verende verbindingen gemodelleerd kunnen worden.

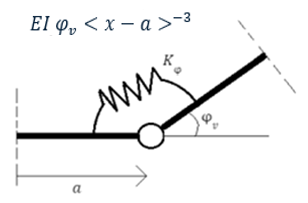
Fig. 15 Modelleren van een roterende verende verbinding (van der Wulp, 2023), correctie (van Gelder, 2024)

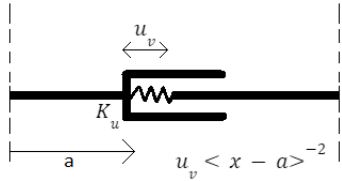
Fig. 16 Modelleren van verende telescoopscharnieren (van der Wulp, 2023)

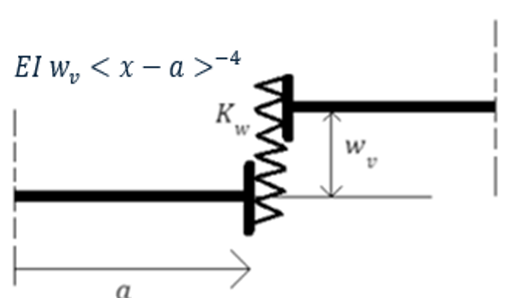
Fig. 17 Modelleren van een translerende verende verbinding (van der Wulp, 2023), correctie (van Gelder, 2024)

De veer wordt dus beschreven als een scharnier met krachten met een grootte van \(F_{\text{veer},V}\), \(F_{\text{veer},N}\), \(T_{\text{veer}}\). Dit kan beschreven worden met singulariteitsfuncties met orde \(-3\) met onbekende grootte \(\Delta \varphi\), \(\Delta u_z\), \(\Delta u_x\) op punt \(\bar x\) in 1D:

(27)\[\begin{split}\begin{align} &q_z\left(x\right) : &EI \ \Delta \varphi \left\langle x - \bar x \right\rangle^{- 3} &+ T_{\text{veer}} \left\langle x - \bar x \right\rangle^{- 2} \\ && EI \ \Delta u_z \left\langle x - \bar x \right\rangle^{- 4} &+ F_{\text{veer},V} \left\langle x - \bar x \right\rangle^{- 1} \\ &q_x\left(x\right) : &EA \ \Delta u_x \left\langle x - \bar x \right\rangle^{- 2} &+ F_{\text{veer},N} \left\langle x - \bar x \right\rangle^{- 1} \\ \end{align}\end{split}\]

In 2D worden de reactiekrachten berekend in het lokale assenstelsel maar moeten deze worden omgeschreven naar het globale assenstelsel in de belastingsvergelijking.

De bijbhorende voorwaardes zijn dan als volgt:

(28)\[\begin{split}\begin{align} &M \left(\bar x\right) = &T_{\text{veer}} = &-K_M \cdot \Delta \varphi \\ &V \left(\bar x\right) = &F_{\text{veer},V} = &-K_V \cdot \Delta u_z \\ &N \left(\bar x\right) = &F_{\text{veer},N} = &-K_N \cdot \Delta u_x \end{align}\end{split}\]

Ook hier is een deels verende verbinding is natuurlijk ook mogelijk met het weglaten van de desbetreffende termen.

Vergelijking voor horizontale en verticale verplaatsingen in 2D

De doorbuiging (\(u_{z}(x)\)) en extensie (\(u_{x}(x)\)) zijn voor tweedimensionale constructies hele abstracte termen die niet bruikbaar zijn voor de oplossingsvoorwaarden. Daarom moeten ze worden gebruikt als invoer voor de vergelijkingen van de horizontale en verticale verplaatsing van de constructie (\(u_{h}(x)\) en \(u_{v}(x)\)). De vergelijkingen stellen telkens dat de invloed van de doorbuiging en extensie van een staaf \(ij\) (\(u_{z,ij}(x)\) en \(u_{x,ij}(x)\)) op \(u_{z}(x)\) en \(u_{z}(x)\) gelijk aan nul is als \(x < a_{i}\), een functie is als \(a_{i} \leq x < a_{j}\) en constant is als \(a_{j} \leq x\). Dit wordt afgebeeld in Figuur Fig. 18 en Fig. 19.

Fig. 18 De invloed van \(u_{x,ij}\left(x\right)\) op \(u_{x}\left(x\right)\) (Baudoin, 2024)

Fig. 19 De invloed van \(u_{z,ij}\left(x\right)\) op \(u_{z}\left(x\right)\) (Baudoin, 2024)

Vervolgens worden \(u_{z,ij}(x)\) en \(u_{x,ij}(x)\) vermenigvuldigd met een functie van de hoek van de staaf wat tot slot voor alle staven wordt opgesomd. Hieruit ontstaan vgl. (29) en (30).

(29)\[\begin{split}u_{v}(x) = u_{z}(0)\cos\left( \theta_{0} \right) - u_{x}(0)\sin\left( \theta_{0} \right) + \sum_{i = 0}^{i = n}\begin{pmatrix}\left( \left( u_{z}(x) - u_{z}\left( a_{i} \right) \right)\left\langle x - a_{i} \right\rangle^{0} - \left( u_{z}(x) - u_{z}\left( a_{j} \right) \right)\left\langle x - a_{j} \right\rangle^{0} \right)\cos\left( \theta_{i} \right) \\ - \left( \left( u_{x}(x) - u_{x}\left( a_{i} \right) \right)\left\langle x - a_{i} \right\rangle^{0} - \left( u_{x}(x) - u_{x}\left( a_{j} \right) \right)\left\langle x - a_{j} \right\rangle^{0} \right)\sin\left( \theta_{i} \right) \end{pmatrix}\end{split}\]

(30)\[\begin{split}u_{h}(x) = u_{z}(0)\sin\left( \theta_{0} \right) + u_{x}(0)\cos\left( \theta_{0} \right) + \sum_{i = 0}^{i = n}\begin{pmatrix} \left( \left( u_{z}(x) - u_{z}\left( a_{i} \right) \right)\left\langle x - a_{i} \right\rangle^{0} - \left( u_{z}(x) - u_{z}\left( a_{j} \right) \right)\left\langle x - a_{j} \right\rangle^{0} \right)\sin\left( \theta_{i} \right) \\+ \left( \left( u_{x}(x) - u_{x}\left( a_{i} \right) \right)\left\langle x - a_{i} \right\rangle^{0} - \left( u_{x}(x) - u_{x}\left( a_{j} \right) \right)\left\langle x - a_{j} \right\rangle^{0} \right)\cos\left( \theta_{i} \right) \end{pmatrix}\end{split}\]

Invloedslijnen met Macaulay

De methode van Macaulay kan worden gebruikt om invloedslijnen te berekenen. In dit hoofdstuk zal worden toegelicht hoe de methode hierbij kan worden ingezet. Hierbij zal de focus liggen op de basis van invloedslijnen met Macaulay, door te beschrijven hoe invloedslijnen berekend kunnen worden voor eendimensionale constructies.

Methode

De eerste stap voor het berekenen van invloedslijnen met de methode van Macaulay is het beschrijven van de krachtsverdeling op de ligger. Hierbij worden alle krachten die op de ligger spelen gedefinieerd op een positie \(x\), waarin \(x\) de variabele is die de positie op de ligger beschrijft. De puntlast waarvoor de invloedslijnen worden bepaald wordt gedefinieerd op een positie \(x = \bar x_F\). Deze methode is weergegeven in figuur Fig. 20.

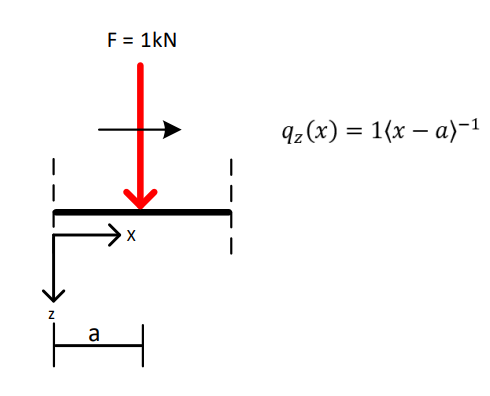
Fig. 20 Methode voor invloedslijnen met Macaulay (Jankie, 2023)

Vervolgens kan de belastingvergelijking worden geïntegreerd naar \(x\). Dit zal resulteren in vergelijkingen met onbekende reactiekrachten en integratieconstanten.

De randvoorwaarden kunnen worden opgesteld. Deze worden gebruikt om de onbekende reactiekrachten en integratieconstanten uit de vergelijkingen op te lossen.

Invullen van de gevonden waardes voor de onbekenden in de geïntegreerde belastingvergelijking resulteert in de gewenste functies. Deze functies hangen af van \(x\) en \(\bar x_F\). Waarin voor \(x\) een positie op de ligger ingevuld kan worden en \(\bar x_F\) de locatie van de puntlast beschrijft. Zo kan de invloed van een puntlast op locatie \(\bar x_F\) op de staafeigenschappen op locatie \(x\) worden bepaald.

Oplossen van geknikte, vertakte en gesloten constructies

De Macaulay methode kan worden uitgebreid zodat het ook toepasbaar is op geknikte, vertakte en gesloten, constructies. De belangrijkste sterktepunten van het model zijn dat het systematisch en robuust is doordat het is gebaseerd op de principes van evenwicht en continuïteit, de snedekrachten en verplaatsingen van elk punt kunnen worden bepaald doordat de functie continue is en dat de oplossingsvoorwaarden geringer in tal en eenvoudiger zijn dan voor de traditionele integratiemethode.

Modelleren van knikken

De belastingen worden in 2D anders gemodelleerd dan in 1D. De vergelijking voor elke belasting wordt voor elke knik aangepast waar de functie van \(x\) langs gaat na het aangrijppunt van de belasting. De hoektermen zijn bepaald door te analyseren wat de invloed is van een hoek op de snedekrachtdiagrammen van een belasting.

Voor elk segment wordt een hoek bepaald, welke kunnen worden samengevoegd in \(\theta \left( \bar x \right)\).

Voor elke kracht \(j\) (voor elke \(F_j\) en \(q_j\) inclusief oplegreacties en krachten uit knooppunten) wordt de belastingsvergelijking aangepast voor elke knik \(i\) met \(n\) het aantal knikken en met een bijbehorende hoek \(\theta \left( \bar x_i \right)\). Daarbij zijn de locaties :

(31)\[\begin{split}\begin{align} &q_z \left( x\right) : &\sum\limits_{j}\sum\limits_{i}^{n} \left\langle \bar x_i - \bar x_{F_j} \right\rangle^{0} &F_{v,j} \left\langle x - \bar x_i \right\rangle^{- 1} &\left( \cos\left( \theta \left( \bar x_i \right) \right) - \cos\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ & &+ \sum\limits_{j}\sum\limits_{i}^n \left\langle \bar x_i - \bar x_{F_j} \right\rangle^{0} &F_{h,j} \left\langle x - \bar x_i \right\rangle^{- 1} &\left( \sin\left( \theta \left( \bar x_i \right) \right) - \sin\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ & &+ \sum\limits_{j}\sum\limits_{i}^n \left\langle \bar x_i - \bar x_{q_j} \right\rangle^{0} &q_{v,j} \left( {\left\langle x - \bar x_i \right\rangle}^{0} + \left\langle x - \bar x_i \right\rangle^{- 1}\left( \bar x_i - \bar x_{q_j} \right) \right) &\left( \cos\left( \theta \left( \bar x_i \right) \right) - \cos\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ & &+ \sum\limits_{j}\sum\limits_{i}^n \left\langle \bar x_i - \bar x_{q_j} \right\rangle^{0} &q_{h,j} \left( {\left\langle x - \bar x_i \right\rangle}^{0} + \left\langle x - \bar x_u \right\rangle^{- 1}\left( \bar x_i - \bar x_{q_j} \right) \right) &\left( \sin\left( \theta \left( \bar x_i \right) \right) - \sin\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ &q_x \left( x\right) : &\sum\limits_{j}\sum\limits_{i}^{n} -\left\langle \bar x_i - \bar x_{F_j} \right\rangle^{0} &F_{v,j} \left\langle x - \bar x_i \right\rangle^{- 1}&\left( \sin\left( \theta \left( \bar x_i \right) \right) - \sin\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ & &+ \sum\limits_{j}\sum\limits_{i}^n \left\langle \bar x_i - \bar x_{F_j} \right\rangle^{0} &F_{h,j} \left\langle x - \bar x_i \right\rangle^{- 1}&\left( \cos\left( \theta \left( \bar x_i \right) \right) - \cos\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ & &+ \sum\limits_{j}\sum\limits_{i}^n -\left\langle \bar x_i - \bar x_{q_j} \right\rangle^{0}&q_{v,j} \left( {\left\langle x - \bar x_i \right\rangle}^{0} + \left\langle x - \bar x_i \right\rangle^{- 1}\left( \bar x_i - \bar x_{q_j} \right) \right)&\left( \sin\left( \theta \left( \bar x_i \right) \right) - \sin\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ & &+ \sum\limits_{j}\sum\limits_{i}^n\left\langle \bar x_i - \bar x_{q_j} \right\rangle^{0} &q_{h,j} \left( {\left\langle x - \bar x_i \right\rangle}^{0} + \left\langle x - \bar x_u \right\rangle^{- 1}\left( \bar x_i - \bar x_{q_j} \right) \right)&\left( \cos\left( \theta \left( \bar x_i \right) \right) - \cos\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \end{align}\end{split}\]

Een koppel heeft geen invloed op de normaal- en dwarskrachten. Verder blijft het buigend moment van een koppel onveranderd bij een knikpunt.

Bij de normaal- en dwarskrachtenlijn van een puntlast ontstaat een sprong als de functie een hoekpunt passeert. Tegelijkertijd ontstaat er een knik in de momentenlijn als de functie een hoekpunt passeert. Deze sprong en knik ontstaan door de verandering van de projectie van de puntlast.

Bij de normaal- en dwarskrachtenlijn van een uniform verdeelde belasting ontstaat zowel een sprong als een knik als de functie een hoekpunt passeert. De knik ontstaat door de verandering van de projectie van de verdeelde belasting. De sprong daarentegen ontstaat door een verandering in de projectie van de arbitrale belasting vervangend puntlast.

Vertakte en gesloten constructies

Met de tot nu toe in dit hoofdstuk verstreken informatie kunnen geknikte constructies worden gemodelleerd met de Macaulay methode. Voor vertakte en gesloten constructies bestaan er drie bijzondere punten met unieke eigenschappen. Dit zijn het knooppunt (\(a_k\)), sprongpunt (\(a_s\)) en aansluitpunt (\(a_a\)).

Fig. 21 Vertakte constructie (Baudoin, 2024)

Fig. 22 Gesloten constructie (Baudoin, 2024)

Knooppunt

Het knooppunt \(\bar x_1\) is het punt waarbij de functie van \(x\) voor het eerst langs een knoop gaat (zoals pijl 1 op knoop B in Fig. 21). Op \(\bar x_1\) moet voor elke staaf waarnaar de functie niet direct de weg vervolgd drie onbekende krachten worden toegevoegd. De formules voor deze krachten volgen bij het hieropvolgende sprongpunt en aansluitpunt.

Sprongpunt

Het sprongpunt, (zie Fig. 23) is het punt waar de functie van \(x\) in het globale assenstelsel een sprong maakt van punt \(\bar x_\text{sprong}\), wat een uiteinde of afsluiting is van een vertakking, naar punt \(\bar x_2\), wat een knoop is waar de functie van \(x\) al eerder langs is geweest (op \(\bar x_1\)). Een voorbeeld is van punt C naar knoop B in figuur Fig. 21. In het lokale assenstelsel verloopt de functie echter continue.

Fig. 23 Modelleren van een sprongpunt (Baudoin, 2024)

Op \(\bar x_1\) moeten de onbekende krachten \(\delta V\), \(\delta H\) en \(\Delta T\) worden toegevoegd waarnaar de functie na de sprong de weg vervolgd. Op \(\bar x_2\) moeten dezelfde krachten weer worden afgetrokken. Verder moeten op \(\bar x_2\) de sprongconstanten \(\Delta \varphi\), \(\Delta u_z\) en \(\Delta u_x\) toegevoegd worden voor de sprong in vervormingen tussen punt \(\bar x_\text{sprong}\) en \(\bar x_2\). Deze worden als volgt gemodelleerd:

(32)\[\begin{split}\begin{align} &q_z\left(x\right) : &\Delta V \left\langle x - \bar x_1 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_1 \right) \right) &- \Delta V \left\langle x - \bar x_2 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_2 \right) \right) \\ & & + \Delta H\left\langle x - \bar x_1 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_1 \right) \right) &- \Delta H\left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x_2 \right) \right) \\ & & +\Delta T \left\langle x - \bar x_1 \right\rangle^{- 2} &- \Delta T \left\langle x - \bar x_2 \right\rangle^{- 2} \\ & &+EI \Delta \varphi \left\langle x - \bar x_2 \right\rangle^{- 3} &+ EI \Delta u_z \left\langle x - \bar x_3 \right\rangle^{- 4} \\ &q_x\left(x\right) : &-\Delta V \left\langle x - \bar x_1 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_1 \right) \right) &+ \Delta V \left\langle x - \bar x_2 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_2 \right) \right)\\ & & + \Delta H\left\langle x - \bar x_1 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_1 \right) \right) &- \Delta H\left\langle x - \bar x_2 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_2 \right) \right) \\ & &&+ EI \Delta u_x \left\langle x - \bar x_2 \right\rangle^{- 2} \end{align}\end{split}\]

De onbekenden kunnen worden opgelost met de volgende vergelijkingen:

(33)\[\begin{split}N\left(\bar x_\text{sprong}^{+}\right) = 0 \\ V\left(\bar x_\text{sprong}^{+}\right) = 0 \\ M\left(\bar x_\text{sprong}^{+}\right) = 0 \\ \varphi\left( \bar x_1 \right) = \varphi \left( \bar x_2 \right) \\ u_v\left( \bar x_1 \right) = u_v \left( \bar x_2 \right) \\ u_h\left( \bar x_1 \right) = u_h \left( \bar x_2 \right)\end{split}\]

Als de functie springt naar een scharnierend verbonden staaf op een knooppunt, dan kunnen de oplosvergelijkingen voor de hoekverdraaiing weggelaten worden. Er hoeven dan ook geen alternatieve voorwaarden worden gesteld.

Aansluitpunt

Het aansluitpunt is het punt waarbij de functie van \(x\) opnieuw langs een knoop gaat (zoals knoop B vanuit punt E in figuur Fig. 22). Dezelfde vergelijkingen als voor een sprongpunt gelden, waarbij \(\Delta \varphi\), \(\Delta u_z\) en \(\Delta u_x\) weg kunnen worden gelaten. Ditmaal is \(\bar x_1\) de eerste keer dat de functie langs de knoop komt en \(\bar x_2\) de twee keer:

(34)\[\begin{split}\begin{align} &q_z\left(x\right) : &\Delta V \left\langle x - \bar x_1 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_1 \right) \right) &- \Delta V \left\langle x - \bar x_2 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_2 \right) \right) \\ & & + \Delta H\left\langle x - \bar x_1 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_1 \right) \right) &- \Delta H\left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x_2 \right) \right) \\ & & +\Delta T \left\langle x - \bar x_1 \right\rangle^{- 2} &- \Delta T \left\langle x - \bar x_2 \right\rangle^{- 2} \\ &q_x\left(x\right) : &-\Delta V \left\langle x - \bar x_1 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_1 \right) \right) &+ \Delta V \left\langle x - \bar x_2 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_2 \right) \right)\\ & & + \Delta H\left\langle x - \bar x_1 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_1 \right) \right) &- \Delta H\left\langle x - \bar x_2 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_2 \right) \right) \\ \end{align}\end{split}\]

De onbekenden kunnen worden opgelost met de volgende vergelijkingen:

(35)\[\begin{split}\varphi\left( \bar x_1 \right) = \varphi \left( \bar x_2 \right) \\ u_v\left( \bar x_1 \right) = u_v \left( \bar x_2 \right) \\ u_h\left( \bar x_1 \right) = u_h \left( \bar x_2 \right)\end{split}\]

Ook hier geldt dat als als de functie scharnierend aansluit op een knooppunt, de oplosvergelijkingen voor de hoekverdraaiing weggelaten kunnen worden. Er hoeven dan ook geen alternatieve voorwaarden worden gesteld.

Overzicht modellering discontinuïteiten

In Table 1 Table 2 (Baudoin, 2024) wordt voorgeschreven welke oplossingsvoorwaarden gelden voor starre onstructies als lokale afstand \(\bar x\) de benoemde eigenschap voor 1D en 2D situaties.

Table 1 Belastingfunctie, vergelijkingen en onbekenden voor discontinuïteiten in 1D

Situatie op \(\bar x\)	Belastingfunctie	Vergelijkingen	Onbekenden
Beginpunt en eindpunt constructie		\(N\left(\bar x^-\right) = 0\) \(V\left(\bar x^-\right) = 0\) \(M\left(\bar x^-\right) = 0\) \(N\left(\bar x\right) = 0\) \(V\left(\bar x^+\right) = 0\) \(M\left(\bar x^+\right) = 0\)	Integratieconstantes \(C_V\), \(C_M\), \(C_N\), \(C_w\), \(C_{\varphi}\), \(C_u\)
Puntlast	\(\begin{align*}&{{q_z\left(x\right) : F \left\langle x - \bar x \right\rangle^{- 1}}}&{{q_x\left(x\right) : F \left\langle x - \bar x \right\rangle^{- 1}}}\end{align*}\)
Koppel	\(q_z\left(x\right) : T \left\langle x - \bar x \right\rangle^{- 2}\)
Verdeelde belasting	\(\begin{align*}&q_z\left(x\right): &q_v \left\langle x - \bar x_1 \right\rangle^{- 1} &-q_v\left\langle x - \bar x_2 \right\rangle^{- 1} \\&q_z\left(x\right): &q_h \left\langle x - \bar x_1 \right\rangle^{- 1} &-q_h\left\langle x - \bar x_2 \right\rangle^{- 1} \end{align*}\) Met \(\bar x_1\) en \(\bar x_2\) het begin en eind van de verdeelde belasting
Scharnier-/schuif-/telescoop-verbinding	\(q_z\left(x\right) : EI \ \Delta \varphi \left\langle x - \bar x \right\rangle^{- 3} \\ q_z\left(x\right) : EI \ \Delta u_z \left\langle x - \bar x \right\rangle^{- 4} \\ q_x\left(x\right) : EA \ \Delta u_x \left\langle x - \bar x \right\rangle^{- 2} \)	\(\begin{align*}M \left(\bar x\right) = 0 \\ V \left(\bar x\right) = 0 \\ N \left(\bar x\right) = 0 \end{align*}\)	\(\Delta \varphi\), \(\Delta u_z\) en \(\Delta u_x\)
Inklemming	\(\begin{align*} &q_z\left(x\right) : &R_{v} \left\langle x - \bar x \right\rangle^{- 1} &+ T \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right) : &R_{h} \left\langle x - \bar x \right\rangle^{- 1} \end{align*}\)	\(R_h\), \(R_v\) en \(T\)
Verende oplegging	\(\begin{align*} &q_z\left(x\right) : &F_{\text{veer},v} \left\langle x - \bar x \right\rangle^{- 1} &+ T_{\text{veer}} \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right) : &F_{\text{veer},h} \left\langle x - \bar x \right\rangle^{- 1} \end{align*}\)	\(\begin{align*}& T_{\text{veer}} = - {K_M} \varphi \ \left( \bar x \right) \\& F_{\text{veer},v} = - {K_V} \ u_v \left(\bar x\right)\\& F_{\text{veer},h} = - {K_N} \ u_h \left(\bar x\right)\end{align*}\)	\(F_{\text{veer},V}\), \(F_{\text{veer},N}\), \(T_{\text{veer}}\)
Verende scharnierverbinding	\(\begin{align*}&q_z\left(x\right) : &EI \ \Delta \varphi \left\langle x - \bar x \right\rangle^{- 3} &+ T_{\text{veer}} \left\langle x - \bar x \right\rangle^{- 2} \\ && EI \ \Delta u_z \left\langle x - \bar x \right\rangle^{- 4} &+ F_{\text{veer},V} \left\langle x - \bar x \right\rangle^{- 1} \\&q_x\left(x\right) : &EA \ \Delta u_x \left\langle x - \bar x \right\rangle^{- 2} &+ F_{\text{veer},N} \left\langle x - \bar x \right\rangle^{- 1} \\ \end{align*}\)	\(\begin{align*}M \left(\bar x\right) = T_{\text{veer}} = -K_M \cdot \Delta \varphi \\V \left(\bar x\right) = F_{\text{veer},V} = -K_V \cdot \Delta u_z \\N \left(\bar x\right) = F_{\text{veer},N} = -K_N \cdot \Delta u_x \end{align*}\)	\(F_{\text{veer},V}\), \(F_{\text{veer},N}\), \(T_{\text{veer}}\), \(\Delta \varphi\), \(\Delta u_z\) en \(\Delta u_x\)

Table 2 Belastingfunctie, vergelijkingen en onbekenden voor discontinuïteiten in 2D

Situatie op \(\bar x\)	Belastingsfunctie	Vergelijkingen	Onbekenden
Beginpunt en eindpunt constructie		\(N\left(\bar x^-\right) = 0\) \(V\left(\bar x^-\right) = 0\) \(M\left(\bar x^-\right) = 0\) \(N\left(\bar x\right) = 0\) \(V\left(\bar x^+\right) = 0\) \(M\left(\bar x^+\right) = 0\)	Integratieconstantes \(C_V\), \(C_M\), \(C_N\), \(C_w\), \(C_{\varphi}\), \(C_u\)
Puntlast	\(\begin{align*} &q_z\left(x\right) : &F_{v} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left(\bar x\right) \right) &+F_{h} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left(\bar x\right) \right) \\ &q_x\left(x\right) : &- F_{v} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta\left(\bar x\right) \right) &+F_{h} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left(\bar x\right) \right) \end{align*}\)
Koppel	\(\begin{align*} &q_z\left(x\right): &T \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right): &0 \end{align*}\)
Verdeelde belasting	\(\begin{align*} &q_z\left(x\right): &q_{v} \left\langle x - \bar x_1 \right\rangle^{- 1} \cos \left( \theta \left(\bar x_1\right) \right) &-q_{v} \left\langle x_2 - \bar x \right\rangle^{- 1} \cos \left( \theta \left(\bar x_2\right) \right) \\ & &+ q_{h} \left\langle x - \bar x_1 \right\rangle^{- 1} \sin \left( \theta \left(\bar x_1\right) \right) &-q_{h} \left\langle x - \bar x_2 \right\rangle^{- 1} \sin \left( \theta \left(\bar x_2\right) \right) \\ & q_x \left(x \right) : &- q_{v} \left\langle x - \bar x_1 \right\rangle^{- 1} \sin \left( \theta \left(\bar x_1\right) \right) &+q_{v} \left\langle x - \bar x_2 \right\rangle^{- 1} \sin \left( \theta \left(\bar x_2\right) \right) \\ &&+q_{h} \left\langle x - \bar x_1 \right\rangle^{- 1} \cos \left( \theta \left(\bar x_1\right) \right) &- q_{h} \left\langle x - \bar x_2 \right\rangle^{- 1} \cos \left( \theta \left(\bar x_2\right) \right) \end{align*}\) Met \(\bar x_1\) en \(\bar x_2\) het begin en eind van de verdeelde belasting
Scharnier-/schuif-/telescoop-verbinding	\(q_z\left(x\right) : EI \ \Delta \varphi \left\langle x - \bar x \right\rangle^{- 3} \\ q_z\left(x\right) : EI \ \Delta u_z \left\langle x - \bar x \right\rangle^{- 4} \\ q_x\left(x\right) : EA \ \Delta u_x \left\langle x - \bar x \right\rangle^{- 2} \)	\(\begin{align*}M \left(\bar x\right) = 0 \\ V \left(\bar x\right) = 0 \\ N \left(\bar x\right) = 0 \end{align*}\)	\(\Delta \varphi\), \(\Delta u_z\) en \(\Delta u_x\)
Inklemming	\(\begin{align*}&q_z\left(x\right) : &R_{v} \left\langle x - \bar x \right\rangle^{- 1} &+ T \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right) : &R_{h} \left\langle x - \bar x \right\rangle^{- 1}\end{align*}\)	\(\begin{align*}\varphi \left( \bar x \right) = 0\\ u_v \left(\bar x\right) = 0\\ u_h \left(\bar x\right) = 0\end{align*}\)	\(R_h\), \(R_v\) en \(T\)
Verende oplegging	\(\begin{align*}&q_z\left(x\right) : &F_{\text{veer},h} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x \right) \right) &+ F_{\text{veer},v} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left( \bar x \right) \right) &+ T_{\text{veer}} \left\langle x - \bar x \right\rangle^{- 2} \\ &q_x\left(x\right) : &R_{\text{veer},h} \left\langle x - \bar x \right\rangle^{- 1}\cos\left( \theta \left( \bar x \right) \right) &- R_{\text{veer},v} \left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x \right) \right)\end{align*}\)	\(\begin{align*}& T_{\text{veer}} = - {K_M} \varphi \ \left( \bar x \right) \\& F_{\text{veer},v} = - {K_V} \ u_v \left(\bar x\right)\\& F_{\text{veer},h} = - {K_N} \ u_h \left(\bar x\right)\end{align*}\)	\(F_{\text{veer},V}\), \(F_{\text{veer},N}\), \(T_{\text{veer}}\)
Verende scharnierverbinding	\(\begin{align*}&q_z\left(x\right) : &EI \ \Delta \varphi \left\langle x - \bar x \right\rangle^{- 3} &+ T_{\text{veer}} \left\langle x - \bar x \right\rangle^{- 2} \\ && EI \ \Delta u_z \left\langle x - \bar x \right\rangle^{- 4} &+ F_{\text{veer},V} \left\langle x - \bar x \right\rangle^{- 1} \\&q_x\left(x\right) : &EA \ \Delta u_x \left\langle x - \bar x \right\rangle^{- 2} &+ F_{\text{veer},N} \left\langle x - \bar x \right\rangle^{- 1} \\ \end{align*}\)	\(\begin{align*}M \left(\bar x\right) = T_{\text{veer}} = -K_M \cdot \Delta \varphi \\V \left(\bar x\right) = F_{\text{veer},V} = -K_V \cdot \Delta u_z \\N \left(\bar x\right) = F_{\text{veer},N} = -K_N \cdot \Delta u_x \end{align*}\)	\(F_{\text{veer},V}\), \(F_{\text{veer},N}\), \(T_{\text{veer}}\), \(\Delta \varphi\), \(\Delta u_z\) en \(\Delta u_x\)
Aansluitpunt	\(\begin{align*}&q_z\left(x\right) : &\Delta V \left\langle x - \bar x_1 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_1 \right) \right) &- \Delta V \left\langle x - \bar x_2 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_2 \right) \right) \\& & + \Delta H\left\langle x - \bar x_1 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_1 \right) \right) &- \Delta H\left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x_2 \right) \right) \\& & +\Delta T \left\langle x - \bar x_1 \right\rangle^{- 2} &- \Delta T \left\langle x - \bar x_2 \right\rangle^{- 2} \\&q_x\left(x\right) : &-\Delta V \left\langle x - \bar x_1 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_1 \right) \right) &+ \Delta V \left\langle x - \bar x_2 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_2 \right) \right)\\& & + \Delta H\left\langle x - \bar x_1 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_1 \right) \right) &- \Delta H\left\langle x - \bar x_2 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_2 \right) \right) \\\end{align*}\) met \(\bar x_1\) de coordinaat van de eerste keer dat langs de vertakking is gegaan en \(\bar x_2\) de tweede keer	\(\begin{align*} \varphi\left( \bar x_1 \right) = \varphi \left( \bar x_2 \right) \\ u_v\left( \bar x_1 \right) = u_v \left( \bar x_2 \right) \\ u_h\left( \bar x_1 \right) = u_h \left( \bar x_2 \right) \end{align*}\)	\(\Delta H\), \(\Delta V\), \(\Delta T\)
Sprongpunt naar andere vertakking	\(\begin{align*}&q_z\left(x\right) : &\Delta V \left\langle x - \bar x_1 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_1 \right) \right) &- \Delta V \left\langle x - \bar x_2 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_2 \right) \right) \\& & + \Delta H\left\langle x - \bar x_1 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_1 \right) \right) &- \Delta H\left\langle x - \bar x \right\rangle^{- 1}\sin\left( \theta \left( \bar x_2 \right) \right) \\& & +\Delta T \left\langle x - \bar x_1 \right\rangle^{- 2} &- \Delta T \left\langle x - \bar x_2 \right\rangle^{- 2} \\& &+EI \Delta \varphi \left\langle x - \bar x_2 \right\rangle^{- 3} &+ EI \Delta u_z \left\langle x - \bar x_3 \right\rangle^{- 4} \\&q_x\left(x\right) : &-\Delta V \left\langle x - \bar x_1 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_1 \right) \right) &+ \Delta V \left\langle x - \bar x_2 \right\rangle^{- 1}\sin\left( \theta \left( \bar x_2 \right) \right)\\& & + \Delta H\left\langle x - \bar x_1 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_1 \right) \right) &- \Delta H\left\langle x - \bar x_2 \right\rangle^{- 1}\cos\left( \theta \left( \bar x_2 \right) \right) \\& &&+ EI \Delta u_x \left\langle x - \bar x_2 \right\rangle^{- 2}\end{align*}\) met \(\bar x_1\) en \(\bar x_2\) de coordinaat van de respectievelijk eerste en tweede keer dat langs de vertakking is gegaan en \(\bar x_\text{sprong}\) de coordinaat voor de sprong.	\(\begin{align*} N\left(\bar x_\text{sprong}^{+}\right) = 0 \\V\left(\bar x_\text{sprong}^{+}\right) = 0 \\M\left(\bar x_\text{sprong}^{+}\right) = 0 \\\varphi\left( \bar x_1 \right) = \varphi \left( \bar x_2 \right) \\u_v\left( \bar x_1 \right) = u_v \left( \bar x_2 \right) \\u_h\left( \bar x_1 \right) = u_h \left( \bar x_2 \right) \end{align*}\)	\(\Delta H\), \(\Delta V\), \(\Delta T\) \(\Delta u_z\), \(\Delta u_x\), \(\Delta \varphi\)
Knikpunt	\( \begin{align*}&q_z \left( x\right) : &\sum\limits_{j}\sum\limits_{i}^{n} \left\langle \bar x_i - \bar x_{F_j} \right\rangle^{0} &F_{v,j} \left\langle x - \bar x_i \right\rangle^{- 1} &\left( \cos\left( \theta \left( \bar x_i \right) \right) - \cos\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\& &+ \sum\limits_{j}\sum\limits_{i}^n \left\langle \bar x_i - \bar x_{F_j} \right\rangle^{0} &F_{h,j} \left\langle x - \bar x_i \right\rangle^{- 1} &\left( \sin\left( \theta \left( \bar x_i \right) \right) - \sin\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\& &+ \sum\limits_{j}\sum\limits_{i}^n \left\langle \bar x_i - \bar x_{q_j} \right\rangle^{0} &q_{v,j} \left( {\left\langle x - \bar x_i \right\rangle}^{0} + \left\langle x - \bar x_i \right\rangle^{- 1}\left( \bar x_i - \bar x_{q_j} \right) \right) &\left( \cos\left( \theta \left( \bar x_i \right) \right) - \cos\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\& &+ \sum\limits_{j}\sum\limits_{i}^n \left\langle \bar x_i - \bar x_{q_j} \right\rangle^{0} &q_{h,j} \left( {\left\langle x - \bar x_i \right\rangle}^{0} + \left\langle x - \bar x_u \right\rangle^{- 1}\left( \bar x_i - \bar x_{q_j} \right) \right) &\left( \sin\left( \theta \left( \bar x_i \right) \right) - \sin\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\&q_x \left( x\right) : &\sum\limits_{j}\sum\limits_{i}^{n} -\left\langle \bar x_i - \bar x_{F_j} \right\rangle^{0} &F_{v,j} \left\langle x - \bar x_i \right\rangle^{- 1}&\left( \sin\left( \theta \left( \bar x_i \right) \right) - \sin\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ & &+ \sum\limits_{j}\sum\limits_{i}^n \left\langle \bar x_i - \bar x_{F_j} \right\rangle^{0} &F_{h,j} \left\langle x - \bar x_i \right\rangle^{- 1}&\left( \cos\left( \theta \left( \bar x_i \right) \right) - \cos\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\& &+ \sum\limits_{j}\sum\limits_{i}^n -\left\langle \bar x_i - \bar x_{q_j} \right\rangle^{0}&q_{v,j} \left( {\left\langle x - \bar x_i \right\rangle}^{0} + \left\langle x - \bar x_i \right\rangle^{- 1}\left( \bar x_i - \bar x_{q_j} \right) \right)&\left( \sin\left( \theta \left( \bar x_i \right) \right) - \sin\left( \theta \left( \bar x_{i-1}^- \right) \right) \right) \\ & &+ \sum\limits_{j}\sum\limits_{i}^n\left\langle \bar x_i - \bar x_{q_j} \right\rangle^{0} &q_{h,j} \left( {\left\langle x - \bar x_i \right\rangle}^{0} + \left\langle x - \bar x_u \right\rangle^{- 1}\left( \bar x_i - \bar x_{q_j} \right) \right)&\left( \cos\left( \theta \left( \bar x_i \right) \right) - \cos\left( \theta \left( \bar x_{i-1}^- \right) \right) \right)\end{align*}\) met \(n\) het aantal knikken met voor elke knik \(i\) een bijbehorende hoek \(\theta_i\) en voor elke \(F_j\) en \(q_j\) inclusing \(H\), \(V\) en \(R\).