Example 3

import micropip
await micropip.install('../../packages/sympy-1.14.dev0-py3-none-any.whl')
#takes a while

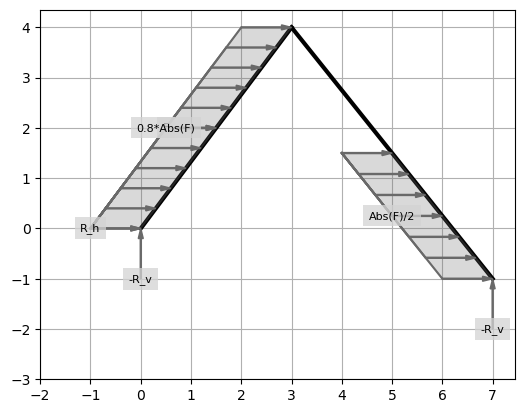
There is a structure containing 2 members. A constant distributed load is applied over the length of the first member. The structure is supported by a pin support at one end and a roller support at the other end. With multiple loads symbolic loads it can be visualized using the draw method.

%pip install git+https://github.com/BorekSaheli/sympy.git@structure2d

import matplotlib.pyplot as plt
from sympy.physics.continuum_mechanics.structure2d import Structure2d
%config InlineBackend.figure_format = 'svg'
from sympy.core.symbol import symbols
E = 3e4
I = 1
A = 1e4
F = symbols("F")
s = Structure2d()
s.add_member(x1=0, y1=0, x2=3, y2=4, E=E, I=I, A=A)
s.add_member(x1=3, y1=4, x2=7, y2=-1, E=E, I=I, A=A)
s.apply_load(start_x=1.5, start_y=2, value=F, global_angle=0, order=-1)
s.apply_load(
    start_x=5,
    start_y=1.5,
    value=F / 2,
    global_angle=s.members[1].angle_deg + 270,
    order=0,
    end_x=7,
    end_y=-1,
)
s.apply_load(
    start_x=0,
    start_y=0,
    value=F * 0.8,
    global_angle=270,
    order=0,
    end_x=3,
    end_y=4,
)
Rv1 = s.apply_support(x=7, y=-1, type="roller")
Rv2, Rh2 = s.apply_support(x=0, y=0, type="pin")
s.solve_for_reaction_loads(Rv1, Rv2, Rh2)
s.draw(show_load_values=True) 

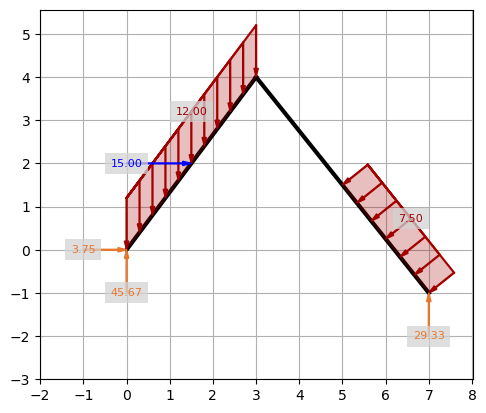
The same plot can be generated without symbols using nummeric values.

E = 3e4
I = 1
A = 1e4
F = 15
s = Structure2d()
s.add_member(x1=0, y1=0, x2=3, y2=4, E=E, I=I, A=A)
s.add_member(x1=3, y1=4, x2=7, y2=-1, E=E, I=I, A=A)
s.apply_load(start_x=1.5, start_y=2, value=F, global_angle=0, order=-1)
s.apply_load(
    start_x=5,
    start_y=1.5,
    value=F / 2,
    global_angle=s.members[1].angle_deg + 270,
    order=0,
    end_x=7,
    end_y=-1,
)
s.apply_load(
    start_x=0,
    start_y=0,
    value=F * 0.8,
    global_angle=270,
    order=0,
    end_x=3,
    end_y=4,
)
Rv1 = s.apply_support(x=7, y=-1, type="roller")
Rv2, Rh2 = s.apply_support(x=0, y=0, type="pin")
s.solve_for_reaction_loads(Rv1, Rv2, Rh2)
s.draw(show_load_values=True)