Example 5

import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

# algemene gegevens
x = sym.symbols('x')
EI, EA = sym.symbols('EI EA')
CV, CM, Cphi, Cuz, CN, Cux = sym.symbols('C_V C_M C_phi C_uz C_N C_ux') 
dx = 2*10**-15

# gegevens constructie
a0, a1, a2, a3, a4, a5 = 0, 4, 8, 12, 16, 20
aa = [a0, a1, a2, a3, a4, a5]
o0, o1, o2, o3, o4 = np.pi/2, 0, 0, -np.pi/2, -np.pi/2
oo = [o0, o1, o2, o3, o4]

# sprongen in de x functie
uzEC, uxEC = sym.symbols('u_z^EC u_x^EC')
s1 = 16+2*dx
ss = [s1]

# gegevens belastingen
qv, qh = 20, 10
RvA, RhA, RvB, RhB, RvC, RhC = sym.symbols('R_v^A R_h^A R_v^B R_h^B R_v^C R_h^C')
phisEB = sym.symbols('phi_s^EB')
VEB, HEB = sym.symbols('V^EB H^EB')
B = [RvA, RhA, qh, -qh, qv, -qv, VEB, HEB, RvC, RhC, -VEB, -HEB, phisEB, uzEC, uxEC, RvB, RhB]
b1, b2, b3, b4, b5, b6, b7 = 0, 4, 8, 12, 16, 16+2*dx, 20
bb = [b1, b1, b1, b2, b2, b4, b3, b3, b5, b5, b6, b6, b6, b6, b6, b7, b7]
# K = 1, Fv = 2, Fh = 3, qv = 4, qh = 5, phi = 6, uz = 7, ux = 8
nn = [2, 3, 5, 5, 4, 4, 2, 3, 2, 3, 2, 3, 6, 7, 8, 2, 3]

#qz opstellen
qz = 0

#beginpunten
for i in range(len(B)):
    for j in range(len(aa)):
        if bb[i] == aa[-1]:
            if nn[i] == 1:
                qz += B[i] * sym.SingularityFunction(x,bb[i],-2)
            if nn[i] == 2:
                qz += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.cos(oo[-1])
            if nn[i] == 3:
                qz += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.sin(oo[-1])
            if nn[i] == 4:
                qz += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.cos(oo[-1])
            if nn[i] == 5:
                qz += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.sin(oo[-1])
            break
        else:
            if bb[i] < aa[j]:
                if nn[i] == 1:
                    qz += B[i] * sym.SingularityFunction(x,bb[i],-2)
                if nn[i] == 2:
                    qz += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.cos(oo[j-1])
                if nn[i] == 3:
                    qz += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.sin(oo[j-1])
                if nn[i] == 4:
                    qz += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.cos(oo[j-1])
                if nn[i] == 5:
                    qz += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.sin(oo[j-1])
                if nn[i] == 6:
                    qz += B[i] * sym.SingularityFunction(x,bb[i],-3) * EI
                if nn[i] == 6:
                    qz += B[i] * sym.SingularityFunction(x,bb[i],-3) * EI
                if nn[i] == 7:
                    qz += B[i] * sym.SingularityFunction(x,bb[i],-4) * EI
                break

# knikpunten
for i in range(len(B)):
    for j in range(len(aa)-1):
        if bb[i] < aa[j]:
            if nn[i] == 2:
                qz += B[i] * sym.SingularityFunction(x,aa[j],-1) * (sym.cos(oo[j]) - sym.cos(oo[j-1]))
            if nn[i] == 3:
                qz += B[i] * sym.SingularityFunction(x,aa[j],-1) * (sym.sin(oo[j]) - sym.sin(oo[j-1]))
            if nn[i] == 4:
                qz += B[i] * ((sym.SingularityFunction(x,aa[j],0) + sym.SingularityFunction(x,aa[j],-1) * (aa[j] - bb[i])) * (sym.cos(oo[j]) - sym.cos(oo[j-1])))
            if nn[i] == 5:
                qz += B[i] * ((sym.SingularityFunction(x,aa[j],0) + sym.SingularityFunction(x,aa[j],-1) * (aa[j] - bb[i])) * (sym.sin(oo[j]) - sym.sin(oo[j-1])))

display(qz)

\[\displaystyle 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{-3} + EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{-4} - 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{-1} + 1.0 H^{EB} {\left\langle x - 16.0 \right\rangle}^{-1} + 1.0 R^{A}_{h} {\left\langle x \right\rangle}^{-1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{-1} - 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{-1} - 1.0 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{-1} - 1.0 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{-1} + 6.12323399573677 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{-1} + 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{-1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{-1} + 6.12323399573677 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{-1} + 6.12323399573677 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{-1} + V^{EB} {\left\langle x - 8 \right\rangle}^{-1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{-1} - 6.12323399573677 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{-1} + 10.0 {\left\langle x \right\rangle}^{0} - 40.0 {\left\langle x - 4 \right\rangle}^{-1} + 10.0 {\left\langle x - 4 \right\rangle}^{0} - 200.0 {\left\langle x - 12 \right\rangle}^{-1} - 20.0 {\left\langle x - 12 \right\rangle}^{0}\]

#qx opstellen
qx = 0

#beginpunten
for i in range(len(B)):
    for j in range(len(aa)):
        if bb[i] == aa[-1]:
            if nn[i] == 2:
                qx += B[i] * sym.SingularityFunction(x,bb[i],-1) * -sym.sin(oo[-1])
            if nn[i] == 3:
                qx += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.cos(oo[-1])
            if nn[i] == 4:
                qx += B[i] * sym.SingularityFunction(x,bb[i],0) * -sym.sin(oo[-1])
            if nn[i] == 5:
                qx += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.cos(oo[-1])
            break
        else:
            if bb[i] < aa[j]:
                if nn[i] == 2:
                    qx += B[i] * sym.SingularityFunction(x,bb[i],-1) * -sym.sin(oo[j-1])
                if nn[i] == 3:
                    qx += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.cos(oo[j-1])
                if nn[i] == 4:
                    qx += B[i] * sym.SingularityFunction(x,bb[i],0) * -sym.sin(oo[j-1])
                if nn[i] == 5:
                    qx += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.cos(oo[j-1])
                if nn[i] == 8:
                    qx += B[i] * sym.SingularityFunction(x,bb[i],-2) * EA
                break

# knikpunten
for i in range(len(B)):
    for j in range(len(aa)-1):
        if bb[i] < aa[j]:
            if nn[i] == 2:
                qx += B[i] * sym.SingularityFunction(x,aa[j],-1) * (-sym.sin(oo[j]) + sym.sin(oo[j-1]))
            if nn[i] == 3:
                qx += B[i] * sym.SingularityFunction(x,aa[j],-1) * (sym.cos(oo[j]) - sym.cos(oo[j-1]))
            if nn[i] == 4:
                qx += B[i] * ((sym.SingularityFunction(x,aa[j],0) + sym.SingularityFunction(x,aa[j],-1) * (aa[j] - bb[i])) * (-sym.sin(oo[j]) + sym.sin(oo[j-1])))
            if nn[i] == 5:
                qx += B[i] * ((sym.SingularityFunction(x,aa[j],0) + sym.SingularityFunction(x,aa[j],-1) * (aa[j] - bb[i])) * (sym.cos(oo[j]) - sym.cos(oo[j-1])))

display(qx)

\[\displaystyle EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{-2} + H^{EB} {\left\langle x - 8 \right\rangle}^{-1} - 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{-1} - 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{-1} + 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{-1} + 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{-1} - 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{-1} + 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{-1} + 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{-1} - 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{-1} + 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{-1} + 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{-1} + 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{-1} + 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{-1} + 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{-1} - 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{-1} + 6.12323399573677 \cdot 10^{-16} {\left\langle x \right\rangle}^{0} + 40.0 {\left\langle x - 4 \right\rangle}^{-1} - 1.77635683940025 \cdot 10^{-15} {\left\langle x - 4 \right\rangle}^{0} + 120.0 {\left\langle x - 12 \right\rangle}^{-1}\]

V = -sym.integrate(qz.expand(), x) + CV
M = sym.integrate(V, x) + CM
kappa = M / EI
phi = sym.integrate(kappa, x) + Cphi
uz = -sym.integrate(phi, x) + Cuz

N = -sym.integrate(qx.expand(), x) + CN
epsilon = N / EA
ux = sym.integrate(epsilon, x) + Cux

uvz = uz.subs(x,0) * sym.cos(o0)
uvx = -ux.subs(x,0) * sym.sin(o0)
for i in range(len(oo)):
    uvz += ((uz - uz.subs(x,aa[i])) * sym.SingularityFunction(x,aa[i],0) - (uz - uz.subs(x,aa[i+1])) * sym.SingularityFunction(x,aa[i+1],0)) * sym.cos(oo[i])
    uvx += -((ux - ux.subs(x,aa[i])) * sym.SingularityFunction(x,aa[i],0) - (ux - ux.subs(x,aa[i+1])) * sym.SingularityFunction(x,aa[i+1],0)) * sym.sin(oo[i])
uv = uvz + uvx

uhz = uz.subs(x,0) * sym.sin(o0)
uhx = ux.subs(x,0) * sym.cos(o0)
for i in range(len(oo)):
    uhz += ((uz - uz.subs(x,aa[i])) * sym.SingularityFunction(x,aa[i],0) - (uz - uz.subs(x,aa[i+1])) * sym.SingularityFunction(x,aa[i+1],0)) * sym.sin(oo[i])
    uhx += ((ux - ux.subs(x,aa[i])) * sym.SingularityFunction(x,aa[i],0) - (ux - ux.subs(x,aa[i+1])) * sym.SingularityFunction(x,aa[i+1],0)) * sym.cos(oo[i])
uh = uhz + uhx

display(sym.symbols('{N}='), N)
display(sym.symbols('{V}='), V)
display(sym.symbols('{M}='), M)
display(sym.symbols('{u_x}='), ux)
display(sym.symbols('{\phi}='), phi)
display(sym.symbols('{u_z}='), uz)
display(sym.symbols('{u_v}='), uv)
display(sym.symbols('{u_h}='), uh)

\[\displaystyle {N}=\]

\[\displaystyle C_{N} - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{-1} - H^{EB} {\left\langle x - 8 \right\rangle}^{0} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{0} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{0} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{0} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{0} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{0} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{0} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{0} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{0} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{0} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{0} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-16} {\left\langle x \right\rangle}^{1} - 40.0 {\left\langle x - 4 \right\rangle}^{0} + 1.77635683940025 \cdot 10^{-15} {\left\langle x - 4 \right\rangle}^{1} - 120.0 {\left\langle x - 12 \right\rangle}^{0}\]

\[\displaystyle {V}=\]

\[\displaystyle C_{V} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{-2} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{-3} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{0} - 1.0 H^{EB} {\left\langle x - 16.0 \right\rangle}^{0} - 1.0 R^{A}_{h} {\left\langle x \right\rangle}^{0} + 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{0} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{0} + 1.0 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{0} + 1.0 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{0} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{0} + 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{0} - V^{EB} {\left\langle x - 8 \right\rangle}^{0} + 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{0} + 6.12323399573677 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{0} - 10.0 {\left\langle x \right\rangle}^{1} + 40.0 {\left\langle x - 4 \right\rangle}^{0} - 10.0 {\left\langle x - 4 \right\rangle}^{1} + 200.0 {\left\langle x - 12 \right\rangle}^{0} + 20.0 {\left\langle x - 12 \right\rangle}^{1}\]

\[\displaystyle {M}=\]

\[\displaystyle C_{M} + C_{V} x - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{-1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{-2} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} - 1.0 H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} + 1.0 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} + 1.0 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - V^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 5.0 {\left\langle x \right\rangle}^{2} + 40.0 {\left\langle x - 4 \right\rangle}^{1} - 5.0 {\left\langle x - 4 \right\rangle}^{2} + 200.0 {\left\langle x - 12 \right\rangle}^{1} + 10.0 {\left\langle x - 12 \right\rangle}^{2}\]

\[\displaystyle {u_x}=\]

\[\displaystyle C_{ux} + \frac{C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}}{EA}\]

\[\displaystyle {\phi}=\]

\[\displaystyle C_{\phi} + \frac{C_{M} x + \frac{C_{V} x^{2}}{2} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{0} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{-1} + 0.5 H^{EB} {\left\langle x - 12 \right\rangle}^{2} - 0.5 H^{EB} {\left\langle x - 16.0 \right\rangle}^{2} - 0.5 R^{A}_{h} {\left\langle x \right\rangle}^{2} + 0.5 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{2} + 0.5 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{2} + 0.5 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{2} + 0.5 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{2} - 3.06161699786838 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{2} - 0.5 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{2} + 0.5 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{2} - 3.06161699786838 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{2} - 3.06161699786838 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{2} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{2}}{2} + 0.5 V^{EB} {\left\langle x - 12 \right\rangle}^{2} + 3.06161699786838 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{2} - 1.66666666666667 {\left\langle x \right\rangle}^{3} + 20.0 {\left\langle x - 4 \right\rangle}^{2} - 1.66666666666667 {\left\langle x - 4 \right\rangle}^{3} + 100.0 {\left\langle x - 12 \right\rangle}^{2} + 3.33333333333333 {\left\langle x - 12 \right\rangle}^{3}}{EI}\]

\[\displaystyle {u_z}=\]

\[\displaystyle - C_{\phi} x + C_{uz} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\]

\[\displaystyle {u_v}=\]

\[\displaystyle - 1.0 C_{ux} + 6.12323399573677 \cdot 10^{-17} C_{uz} + 6.12323399573677 \cdot 10^{-17} \left(- C_{\phi} x - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\right) {\left\langle x \right\rangle}^{0} + 1.0 \left(- \frac{4 C_{N} - 2.44929359829471 \cdot 10^{-16} R^{A}_{h} + 4.0 R^{A}_{v} - 4.89858719658941 \cdot 10^{-15}}{EA} + \frac{C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 4 \right\rangle}^{0} + 1.0 \left(- \frac{12 C_{N} - 4 H^{EB} - 8.0 R^{A}_{h} + 4.0 R^{A}_{v} - 320.0}{EA} + \frac{C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 12 \right\rangle}^{0} - 1.0 \left(- \frac{20 C_{N} - EA u^{EC}_{x} - 4.0 H^{EB} - 8.0 R^{A}_{h} - 2.44929359829471 \cdot 10^{-16} R^{C}_{h} - 4.0 R^{A}_{v} - 4.0 R^{C}_{v} - 4.0 V^{EB} - 1600.0}{EA} + \frac{C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 20 \right\rangle}^{0} + 1.0 \left(- C_{\phi} x + 4 C_{\phi} + \frac{8 C_{M} + \frac{32 C_{V}}{3} - 10.6666666666667 R^{A}_{h} - 6.53144959545255 \cdot 10^{-16} R^{A}_{v} - 106.666666666667}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\right) {\left\langle x - 4 \right\rangle}^{0} - 1.0 \left(- C_{\phi} x + 12 C_{\phi} + \frac{72 C_{M} + 288 C_{V} - 202.666666666667 R^{A}_{h} - 85.3333333333333 R^{A}_{v} - \frac{32 V^{EB}}{3} - 6933.33333333333}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\right) {\left\langle x - 12 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-17} \left(- C_{\phi} x + 20 C_{\phi} + \frac{200 C_{M} + \frac{4000 C_{V}}{3} - 7.99999999999999 EI \phi^{EB}_{s} - EI u^{EC}_{z} + 74.6666666666667 H^{EB} - 565.333333333333 R^{A}_{h} + 10.6666666666667 R^{C}_{h} - 597.333333333333 R^{A}_{v} - 6.53144959545255 \cdot 10^{-16} R^{C}_{v} - 202.666666666667 V^{EB} - 46186.6666666667}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\right) {\left\langle x - 20 \right\rangle}^{0} - \frac{1.0 \left(C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}\right) {\left\langle x \right\rangle}^{0}}{EA}\]

\[\displaystyle {u_h}=\]

\[\displaystyle 6.12323399573677 \cdot 10^{-17} C_{ux} + 1.0 C_{uz} + 1.0 \left(- C_{\phi} x - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\right) {\left\langle x \right\rangle}^{0} + 1.0 \left(- \frac{4 C_{N} - 2.44929359829471 \cdot 10^{-16} R^{A}_{h} + 4.0 R^{A}_{v} - 4.89858719658941 \cdot 10^{-15}}{EA} + \frac{C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 4 \right\rangle}^{0} - 1.0 \left(- \frac{12 C_{N} - 4 H^{EB} - 8.0 R^{A}_{h} + 4.0 R^{A}_{v} - 320.0}{EA} + \frac{C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 12 \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-17} \left(- \frac{20 C_{N} - EA u^{EC}_{x} - 4.0 H^{EB} - 8.0 R^{A}_{h} - 2.44929359829471 \cdot 10^{-16} R^{C}_{h} - 4.0 R^{A}_{v} - 4.0 R^{C}_{v} - 4.0 V^{EB} - 1600.0}{EA} + \frac{C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 20 \right\rangle}^{0} - 1.0 \left(- C_{\phi} x + 4 C_{\phi} + \frac{8 C_{M} + \frac{32 C_{V}}{3} - 10.6666666666667 R^{A}_{h} - 6.53144959545255 \cdot 10^{-16} R^{A}_{v} - 106.666666666667}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\right) {\left\langle x - 4 \right\rangle}^{0} - 1.0 \left(- C_{\phi} x + 12 C_{\phi} + \frac{72 C_{M} + 288 C_{V} - 202.666666666667 R^{A}_{h} - 85.3333333333333 R^{A}_{v} - \frac{32 V^{EB}}{3} - 6933.33333333333}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\right) {\left\langle x - 12 \right\rangle}^{0} + 1.0 \left(- C_{\phi} x + 20 C_{\phi} + \frac{200 C_{M} + \frac{4000 C_{V}}{3} - 7.99999999999999 EI \phi^{EB}_{s} - EI u^{EC}_{z} + 74.6666666666667 H^{EB} - 565.333333333333 R^{A}_{h} + 10.6666666666667 R^{C}_{h} - 597.333333333333 R^{A}_{v} - 6.53144959545255 \cdot 10^{-16} R^{C}_{v} - 202.666666666667 V^{EB} - 46186.6666666667}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{EB}_{s} {\left\langle x - 16.0 \right\rangle}^{1} - EI u^{EC}_{z} {\left\langle x - 16.0 \right\rangle}^{0} + 0.166666666666667 H^{EB} {\left\langle x - 12 \right\rangle}^{3} - 0.166666666666667 H^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.166666666666667 R^{A}_{h} {\left\langle x \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3} + 0.166666666666667 R^{B}_{h} {\left\langle x - 20 \right\rangle}^{3} + 0.166666666666667 R^{C}_{h} {\left\langle x - 16 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{A}_{v} {\left\langle x \right\rangle}^{3} - 0.166666666666667 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{3} + 0.166666666666667 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{B}_{v} {\left\langle x - 20 \right\rangle}^{3} - 1.02053899928946 \cdot 10^{-17} R^{C}_{v} {\left\langle x - 16 \right\rangle}^{3} - \frac{V^{EB} {\left\langle x - 8 \right\rangle}^{3}}{6} + 0.166666666666667 V^{EB} {\left\langle x - 12 \right\rangle}^{3} + 1.02053899928946 \cdot 10^{-17} V^{EB} {\left\langle x - 16.0 \right\rangle}^{3} - 0.416666666666667 {\left\langle x \right\rangle}^{4} + 6.66666666666667 {\left\langle x - 4 \right\rangle}^{3} - 0.416666666666667 {\left\langle x - 4 \right\rangle}^{4} + 33.3333333333333 {\left\langle x - 12 \right\rangle}^{3} + 0.833333333333333 {\left\langle x - 12 \right\rangle}^{4}}{EI}\right) {\left\langle x - 20 \right\rangle}^{0} + \frac{6.12323399573677 \cdot 10^{-17} \left(C_{N} x - EA u^{EC}_{x} {\left\langle x - 16.0 \right\rangle}^{0} - H^{EB} {\left\langle x - 8 \right\rangle}^{1} + 1.0 H^{EB} {\left\langle x - 12 \right\rangle}^{1} + 6.12323399573677 \cdot 10^{-17} H^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{A}_{h} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{h} {\left\langle x - 4 \right\rangle}^{1} + 1.0 R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{B}_{h} {\left\langle x - 20 \right\rangle}^{1} - 6.12323399573677 \cdot 10^{-17} R^{C}_{h} {\left\langle x - 16 \right\rangle}^{1} + 1.0 R^{A}_{v} {\left\langle x \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 4 \right\rangle}^{1} - 1.0 R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - 1.0 R^{B}_{v} {\left\langle x - 20 \right\rangle}^{1} - 1.0 R^{C}_{v} {\left\langle x - 16 \right\rangle}^{1} - 1.0 V^{EB} {\left\langle x - 12 \right\rangle}^{1} + 1.0 V^{EB} {\left\langle x - 16.0 \right\rangle}^{1} - 3.06161699786838 \cdot 10^{-16} {\left\langle x \right\rangle}^{2} - 40.0 {\left\langle x - 4 \right\rangle}^{1} + 8.88178419700125 \cdot 10^{-16} {\left\langle x - 4 \right\rangle}^{2} - 120.0 {\left\langle x - 12 \right\rangle}^{1}\right) {\left\langle x \right\rangle}^{0}}{EA}\]

# 6 reactiekrachten + 2 knoopkrachten + 2 vervormingssprongen + 1 scharnier + 6 integratieconstanten = 17 voorwaarden
Eq1 = sym.Eq(N.subs(x,0-dx),0)
Eq2 = sym.Eq(N.subs(x,a4),0)
Eq3 = sym.Eq(N.subs(x,a5),0)
Eq4 = sym.Eq(V.subs(x,0-dx),0)
Eq5 = sym.Eq(V.subs(x,a4),0)
Eq6 = sym.Eq(V.subs(x,a5),0)
Eq7 = sym.Eq(M.subs(x,0),0)
Eq8 = sym.Eq(M.subs(x,a4),0)
Eq9 = sym.Eq(M.subs(x,a5),0)
Eq10 = sym.Eq(uv.subs(x,0),0)
Eq11 = sym.Eq(uv.subs(x,a4),0)
Eq12 = sym.Eq(uv.subs(x,a5),0)
Eq13 = sym.Eq(uh.subs(x,0),0)
Eq14 = sym.Eq(uh.subs(x,a4),0)
Eq15 = sym.Eq(uh.subs(x,a5),0)
Eq16 = sym.Eq(uv.subs(x,s1)-uv.subs(x,a2),0)
Eq17 = sym.Eq(uh.subs(x,s1)-uh.subs(x,a2),0)

sol = sym.solve((Eq1,Eq2,Eq3,Eq4,Eq5,Eq6,Eq7,Eq8,Eq9,Eq10,Eq11,Eq12,Eq13,Eq14,Eq15,Eq16,Eq17),(RvA,RhA,RvB,RhB,RvC,RhC,VEB,HEB,phisEB,uzEC,uxEC,CN,CV,CM,Cphi,Cuz,Cux))
display(sol)

{C_M: 0.0,
 C_N: 0.0,
 C_V: 0.0,
 C_phi: (-4.35200000000004e+259*EA**3 - 6.24000000000002e+259*EA**2*EI - 1.4112e+259*EA*EI**2 - 1.62e+257*EI**3)/(2.688e+257*EA**3*EI + 3.744e+257*EA**2*EI**2 + 1.62e+256*EA*EI**3),
 C_ux: 0.0,
 C_uz: 0.0,
 H^EB: (-2.82440737464642e+213*EA**2 - 3.45057316053499e+213*EA*EI - 1.44884104713583e+212*EI**2)/(2.24e+227*EA**2 + 3.12e+227*EA*EI + 1.35e+226*EI**2),
 R_h^A: (-5.76000000000005e+228*EA**2 - 6.54e+228*EA*EI - 5.4e+227*EI**2)/(2.24e+227*EA**2 + 3.12e+227*EA*EI + 1.35e+226*EI**2),
 R_h^B: (-1.85250730654591e+275*EA**2 - 2.53045465343985e+275*EA*EI - 1.09035331709877e+274*EI**2)/(2.24e+289*EA**2 + 3.12e+289*EA*EI + 1.35e+288*EI**2),
 R_h^C: (-3.19999999999995e+228*EA**2 - 5.94e+228*EA*EI - 3.65932793530848e+211*EI**2)/(2.24e+227*EA**2 + 3.12e+227*EA*EI + 1.35e+226*EI**2),
 R_v^A: (-5.91999999999986e+228*EA**2 - 1.26e+229*EA*EI - 5.85e+227*EI**2)/(2.24e+227*EA**2 + 3.12e+227*EA*EI + 1.35e+226*EI**2),
 R_v^B: (-1.95200000000003e+291*EA**2 - 1.848e+291*EA*EI - 7.19999999999999e+289*EI**2)/(2.24e+289*EA**2 + 3.12e+289*EA*EI + 1.35e+288*EI**2),
 R_v^C: (-1.03999999999999e+229*EA**2 - 1.884e+229*EA*EI - 8.55e+227*EI**2)/(2.24e+227*EA**2 + 3.12e+227*EA*EI + 1.35e+226*EI**2),
 V^EB: (-1.95200000000003e+229*EA**2 - 1.848e+229*EA*EI - 7.19999999999999e+227*EI**2)/(2.24e+227*EA**2 + 3.12e+227*EA*EI + 1.35e+226*EI**2),
 phi_s^EB: (-2.80832777782885e+303*EA**3 - 4.15983552090897e+303*EA**2*EI + 1.95485941409754e+303*EA*EI**2 - 2.65612140092532e+286*EI**3)/(1.4743720833598e+302*EA**3*EI + 2.05358968753686e+302*EA**2*EI**2 + 8.88572460953451e+300*EA*EI**3),
 u_x^EC: (-2.01320441798697e+284*EA**3 - 9.76000000000014e+299*EA**2*EI - 9.23999999999999e+299*EA*EI**2 - 3.59999999999999e+298*EI**3)/(2.8e+297*EA**3*EI + 3.9e+297*EA**2*EI**2 + 1.6875e+296*EA*EI**3),
 u_z^EC: (-1.13231776002033e+355*EA**3 - 1.67151669336335e+355*EA**2*EI - 1.99672105003585e+354*EA*EI**2 - 5.68686375010208e+352*EI**3)/(2.35899533337568e+352*EA**3*EI + 3.28574350005898e+352*EA**2*EI**2 + 1.42171593752552e+351*EA*EI**3)}

#display(sym.simplify(uz.subs(sol).rewrite(sym.Piecewise)))
ea = 10**3
ei = 10**3

display(f'{RvA} = {RvA.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{RhA} = {RhA.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{RvB} = {RvB.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{RhB} = {RhB.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{RvC} = {RvC.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{RhC} = {RhC.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')

display(f'{VEB} = {VEB.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{HEB} = {HEB.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')

display(f'{phisEB} = {phisEB.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')

display(f'{uzEC} = {uzEC.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')
display(f'{uxEC} = {uxEC.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')

display(f'{CN} = {CN.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{CV} = {CV.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{CM} = {CM.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{Cphi} = {Cphi.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')
display(f'{Cux} = {Cux.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')
display(f'{Cuz} = {Cuz.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')

'R_v^A = -34.77'

'R_h^A = -23.37'

'R_v^B = -70.46'

'R_h^B = -0.00'

'R_v^C = -54.77'

'R_h^C = -16.63'

'V^EB = -70.46'

'H^EB = -0.00'

'phi_s^EB = -0.0139'

'u_z^EC = -0.5200'

'u_x^EC = -0.2819'

'C_N = 0.00'

'C_V = 0.00'

'C_M = 0.00'

'C_phi = -0.1823'

'C_ux = 0.0000'

'C_uz = 0.0000'

vEC, hEC = sym.symbols('v^EC h^EC')
vv = [vEC]
hh = [hEC]
v = 0
h = 0
for i in range(len(oo)):
    v += -(sym.SingularityFunction(x,aa[i],1) - sym.SingularityFunction(x,aa[i+1],1)) * sym.sin(oo[i])
    h += (sym.SingularityFunction(x,aa[i],1) - sym.SingularityFunction(x,aa[i+1],1)) * sym.cos(oo[i])
for i in range(len(ss)):
    v += vv[i] * sym.SingularityFunction(x,ss[i],0)
    h += hh[i] * sym.SingularityFunction(x,ss[i],0)

# 2 x 2 sprongen = 4 onbekenden
Eq1 = sym.Eq(v.subs(x,a2),v.subs(x,s1))
Eq2 = sym.Eq(h.subs(x,a2),h.subs(x,s1))

sol2 = sym.solve((Eq1,Eq2),(vEC, hEC))
display(sol2)

{h^EC: -4.00000000000000, v^EC: -4.00000000000000}

L = aa[-1]
x_np = np.linspace(0-dx,L+dx,10000)
ab = aa
ab.extend(bb)
ab.sort()
ab = list(dict.fromkeys(ab))

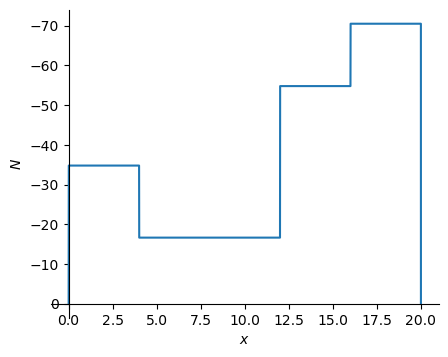
N_np = sym.lambdify(x, N.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))
display(N.subs(sol).subs(EI,ei).subs(EA,ea))

for i in range(len(ab)):
    display(f'N({ab[i]}) = {N.subs(x,ab[i]).subs(sol).subs(EI,ei).subs(EA,ea)} [kN]')

plt.figure(figsize=(5,4))
plt.plot(x_np,N_np(x_np))
plt.xlabel('$x$')
plt.ylabel('$N$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()

\[\displaystyle - 34.7679708826203 {\left\langle x \right\rangle}^{0} - 6.12323399573677 \cdot 10^{-16} {\left\langle x \right\rangle}^{1} + 18.1346678798907 {\left\langle x - 4 \right\rangle}^{0} + 1.77635683940025 \cdot 10^{-15} {\left\langle x - 4 \right\rangle}^{1} + 1.1683102165414 \cdot 10^{-14} {\left\langle x - 8 \right\rangle}^{0} - 38.1346678798906 {\left\langle x - 12 \right\rangle}^{0} + 54.7679708826203 {\left\langle x - 16 \right\rangle}^{0} + 281.856232939038 {\left\langle x - 16.0 \right\rangle}^{-1} - 70.4640582347594 {\left\langle x - 16.0 \right\rangle}^{0} + 70.4640582347594 {\left\langle x - 20 \right\rangle}^{0}\]

'N(0) = -34.7679708826203 [kN]'

'N(4) = -16.6333030027296 [kN]'

'N(8) = -16.6333030027296 [kN]'

'N(12) = -54.7679708826203 [kN]'

'N(16) = 2.94402054944811E-14 [kN]'

'N(16.000000000000004) = oo [kN]'

'N(20) = 2.94402054944811E-14 [kN]'

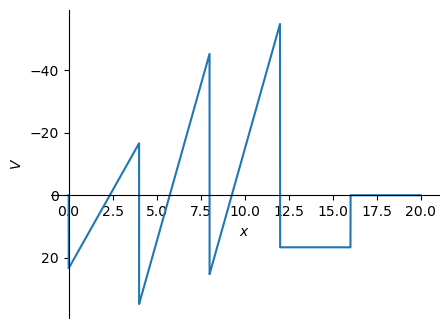
V_np = sym.lambdify(x, V.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))
display(V.subs(sol).subs(EI,ei).subs(EA,ea))

for i in range(len(ab)):
    display(f'V({ab[i]}) = {V.subs(x,ab[i]+dx).subs(sol).subs(EI,ei).subs(EA,ea)} [kN]')

plt.figure(figsize=(5,4))
plt.plot(x_np,V_np(x_np))
plt.xlabel('$x$')
plt.ylabel('$V$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()

\[\displaystyle 23.3666969972704 {\left\langle x \right\rangle}^{0} - 10.0 {\left\langle x \right\rangle}^{1} + 51.40127388535 {\left\langle x - 4 \right\rangle}^{0} - 10.0 {\left\langle x - 4 \right\rangle}^{1} + 70.4640582347594 {\left\langle x - 8 \right\rangle}^{0} + 71.40127388535 {\left\langle x - 12 \right\rangle}^{0} + 20.0 {\left\langle x - 12 \right\rangle}^{1} - 16.6333030027297 {\left\langle x - 16 \right\rangle}^{0} + 520.000000000003 {\left\langle x - 16.0 \right\rangle}^{-3} + 27.7221716712255 {\left\langle x - 16.0 \right\rangle}^{-2} + 7.36842299680748 \cdot 10^{-15} {\left\langle x - 16.0 \right\rangle}^{0} - 3.86002017933822 \cdot 10^{-15} {\left\langle x - 20 \right\rangle}^{0}\]

'V(0) = 23.3666969972703 [kN]'

'V(4) = 34.7679708826203 [kN]'

'V(8) = 25.2320291173797 [kN]'

'V(12) = 16.6333030027296 [kN]'

'V(16) = oo [kN]'

'V(16.000000000000004) = -1.05499772028045E-14 [kN]'

'V(20) = -5.59732895374049E-14 [kN]'

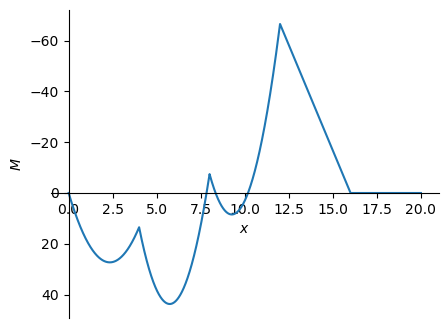
M_np = sym.lambdify(x, M.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))

for i in range(len(ab)):
    display(f'M({ab[i]}) = {M.subs(x,ab[i]).subs(sol).subs(EI,ei).subs(EA,ea)} [kNm]')

plt.figure(figsize=(5,4))
plt.plot(x_np,M_np(x_np))
plt.xlabel('$x$')
plt.ylabel('$M$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()

'M(0) = 0.0 [kNm]'

'M(4) = 13.4667879890814 [kNm]'

'M(8) = -7.46132848043729 [kNm]'

'M(12) = -66.5332120109185 [kNm]'

'M(16) = 5.68434188608080E-14 [kNm]'

'M(16.000000000000004) = oo [kNm]'

'M(20) = 1.27101121769055E-13 [kNm]'

v_np = sym.lambdify(x, v.subs(sol2).rewrite(sym.Piecewise))
h_np = sym.lambdify(x, h.subs(sol2).rewrite(sym.Piecewise))

uv_np = sym.lambdify(x, uv.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))
uh_np = sym.lambdify(x, uh.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))

#display(uv.subs(sol))
for i in range(len(ab)):
    display(f'uv({ab[i]:.1f}) = {uv.subs(x,ab[i]).subs(sol).subs(EI,ei).subs(EA,ea):.4f} [m]')

for i in range(len(ab)):
    display(f'uh({ab[i]:.1f}) = {uh.subs(x,ab[i]).subs(sol).subs(EI,ei).subs(EA,ea):.4f} [m]')

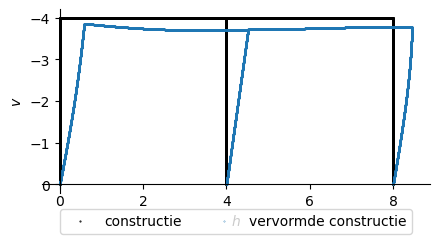
plt.figure(figsize=(5,4))
plt.plot(h_np(x_np),v_np(x_np), marker='.',markersize=1, linewidth=0, color='black', label='constructie')
plt.plot((h_np(x_np)+uh_np(x_np)),(v_np(x_np)+uv_np(x_np)), marker='.',markersize=0.5, linewidth=0, label='vervormde constructie')
plt.xlabel('$h$')
plt.ylabel('$v$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
plt.axis('scaled')
ax.legend(loc='upper center', bbox_to_anchor=(0.5, -0.05),fancybox=True, shadow=False, ncol=3);

'uv(0.0) = 0.0000 [m]'

'uv(4.0) = 0.1391 [m]'

'uv(8.0) = 0.2819 [m]'

'uv(12.0) = 0.2191 [m]'

'uv(16.0) = 0.0000 [m]'

'uv(16.0) = 0.2819 [m]'

'uv(20.0) = 0.0000 [m]'

'uh(0.0) = 0.0000 [m]'

'uh(4.0) = 0.5865 [m]'

'uh(8.0) = 0.5200 [m]'

'uh(12.0) = 0.4535 [m]'

'uh(16.0) = 0.0000 [m]'

'uh(16.0) = 0.5200 [m]'

'uh(20.0) = 0.0000 [m]'