Varianten

Varianten#

import sympy as sp
import numpy as np
from sympy import symbols
sf = sp.SingularityFunction
import matplotlib.pyplot as plt

x = np.linspace(0, 4, 20)

y = x**2
hell = 2*x

fig = plt.figure(figsize=(10, 5))
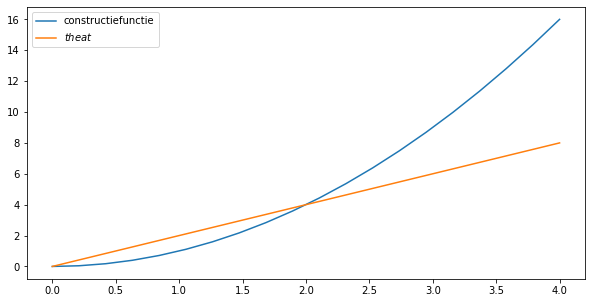
plt.plot(x, y, label='constructiefunctie')
plt.plot(x, hell, label="$theat$")
plt.legend()
plt.savefig('gelobale theta', dpi=450);
../../_images/a30b3d38d219400c6e787256078a4d00c6d9f7e6eb5b1129c03e42365561dfc7.png 
EI = symbols('EI')
x = symbols('x')

Cv, Cm, Cphi, Cw, Av, Bv, Ah, Cn = sp.symbols('Cv, Cm, Cphi, Cw, Av, Bv, Ah, Cn')

# Define F and l
F = 10  ## KN
l = 4   ## m
theta = x/10

# Define qz and qx
qz = -Av * sf(x, 0, -1) + F * sf(x, l/2, -1) - Bv * sf(x, l, -1)
qx = Ah * sf(x, 0, -1)

Variant 1#

#V = sp.integrate(-qx * sp.sin(theta), x) + sp.integrate(-qz * sp.cos(theta), x) + Cv
#N = sp.integrate(-qx * sp.cos(theta), x) + sp.integrate(qz * sp.sin(theta), x) + Cn
#M = sp.integrate(V/sp.cos(theta), x) + Cm
#phi = sp.integrate(M, x) + Cphi
#W = sp.integrate(-phi, x) + Cw

## Pyhton Reageert niet meer

Variant 2#

cos_theta = 1 - (theta**2/sp.factorial(2)) + (theta**4/sp.factorial(4)) - (theta**6/sp.factorial(6))
sin_theta = theta - (theta**3/sp.factorial(3)) + (theta**5/sp.factorial(5)) - (theta**7/sp.factorial(7))

#V = sp.integrate(-qx * sin_theta, x) + sp.integrate(-qz * cos_theta, x) + Cv
#N = sp.integrate(-qx * cos_theta, x) + sp.integrate(qz * sin_theta, x) + Cn

#M = sp.integrate(V/cos_theta, x) + Cm
#phi = sp.integrate(M, x) + Cphi
#W = sp.integrate(-phi, x) + Cw

## python geeft een error bij het integreren

Variant 3#

#V = sp.integrate(-qx , x) * sp.integrate(sp.sin(theta), x) + sp.integrate(-qz, x)* sp.integrate(sp.cos(theta), x) + Cv
#N = sp.integrate(-qx, x)* sp.integrate(sp.cos(theta), x) + sp.integrate(qz, x) * sp.integrate(sp.sin(theta), x) + Cn
#M = sp.integrate(V, x) / (sp.integrate(sp.cos(theta), x)) + Cm
#phi = sp.integrate(M, x) + Cphi
#W = sp.integrate(-phi, x) + Cw

Variant 4#

#V = sp.integrate(-qx , x) * sp.integrate(sin_theta, x) + sp.integrate(-qz, x)* sp.integrate(cos_theta, x) + Cv
#N = sp.integrate(-qx, x)* sp.integrate(cos_theta, x) + sp.integrate(qz, x) * sp.integrate(sin_theta, x) + Cn
#M = sp.integrate(V, x) / (sp.integrate(cos_theta, x)) + Cm
#phi = sp.integrate(M, x) + Cphi
#W = sp.integrate(-phi, x) + Cw
Contents