Eendimensionale voorbeelden

Eendimensionale voorbeelden#

import sympy as sp
import numpy as np
from sympy import symbols
E, I = symbols('E, I')
x = symbols('x')
a = symbols('a')
sf = sp.SingularityFunction
import matplotlib.pyplot as plt

# Voorbeeld 1
w_influence = (-1/6)*(1/10)*sf(10, a, 1)*sf(x, 0, 3) + 1/6*sf(x, a, 3) - (1/6)*(1 - (1/10)*sf(10, a, 1))*sf(x, 10, 3) - (-(5/3)*sf(10, a, 1) + (1/60)*sf(10, a, 3))*x
phi = sp.diff(w_influence, x)*-1
M = sp.diff(phi, x)
V = sp.diff(M, x)

x_value = 8
a_value = 5

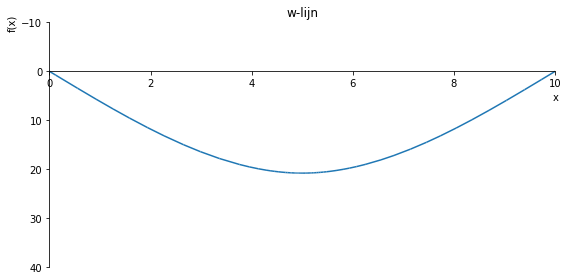
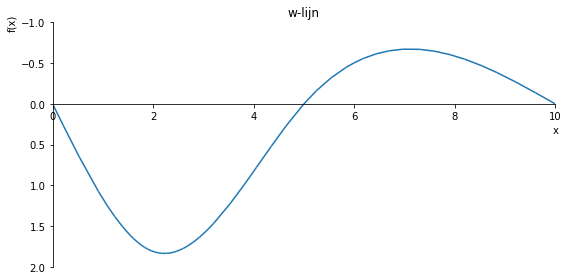
sp.plot(w_influence.subs(a, a_value), ylim=(40, -10), xlim=(0, 10), size=(8, 4), title='w-lijn')
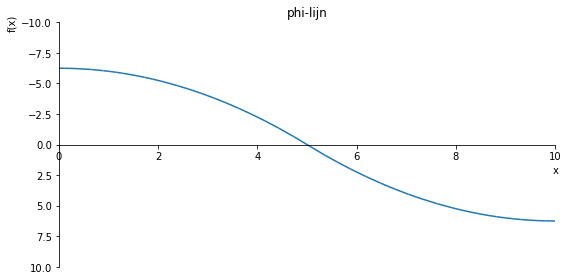
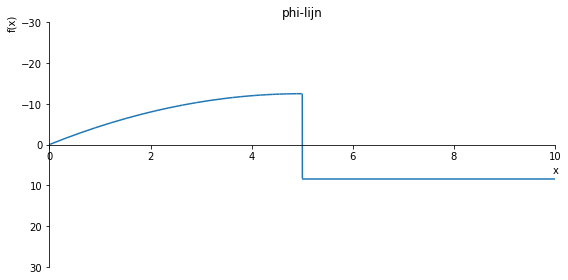
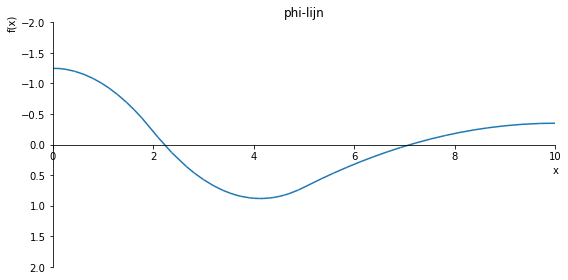
sp.plot(phi.subs(a, a_value), ylim=(10, -10), xlim=(0, 10), size=(8, 4), title='phi-lijn')
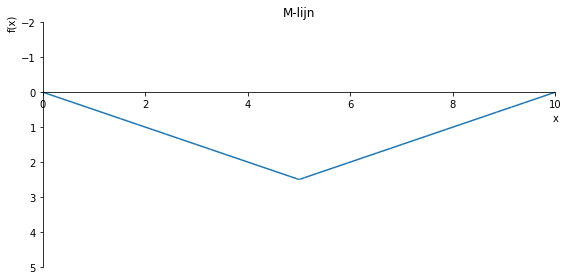
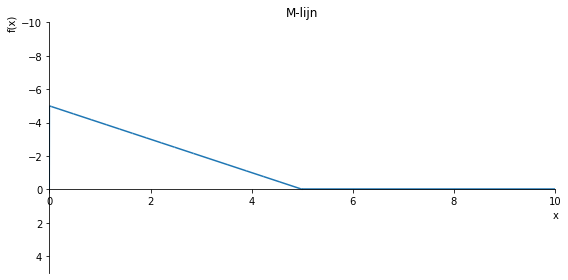
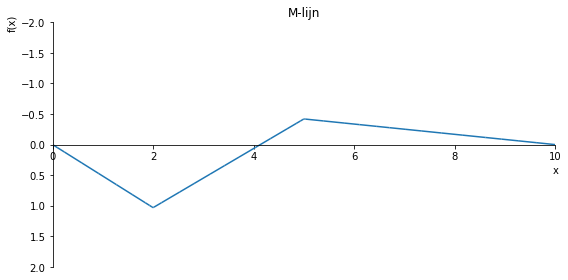
sp.plot(M.subs(a, a_value), ylim=(5, -2), xlim=(0, 10), size=(8, 4), title='M-lijn')
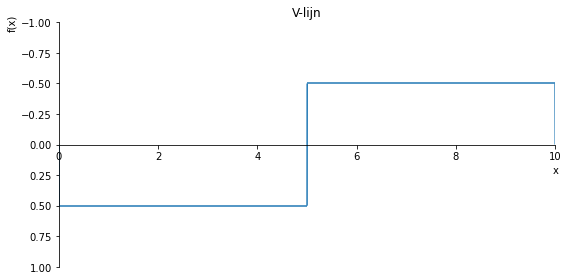
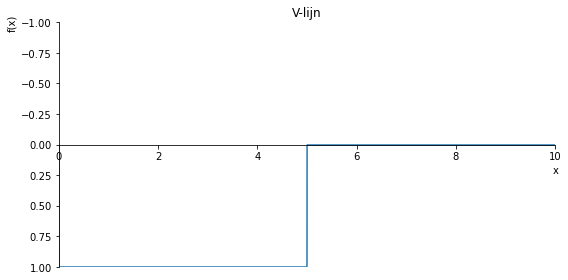
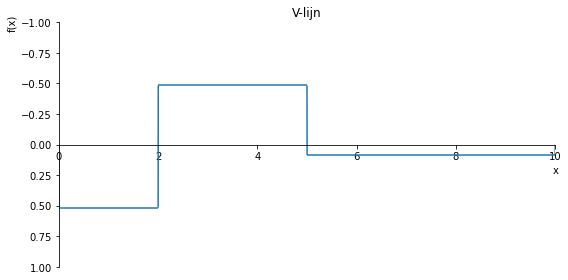
sp.plot(V.subs(a, a_value), ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='V-lijn')

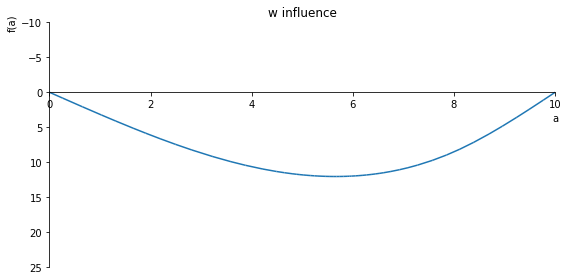
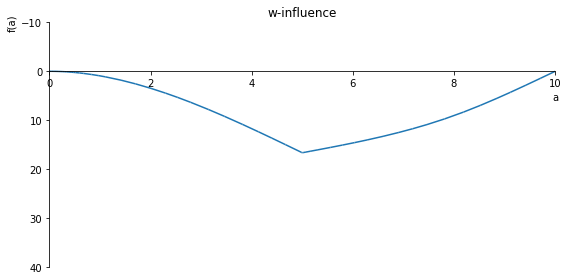
sp.plot(w_influence.subs(x, x_value), ylim=(25, -10), xlim=(0, 10), size=(8, 4), title='w influence')
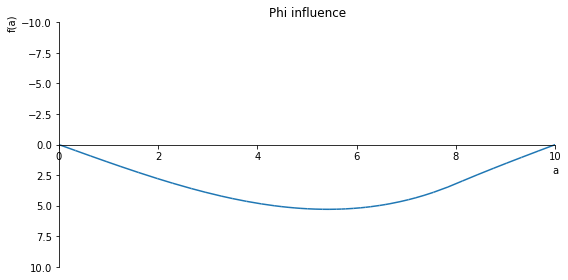
sp.plot(phi.subs(x, x_value), ylim=(10, -10), xlim=(0, 10), size=(8, 4), title='Phi influence')
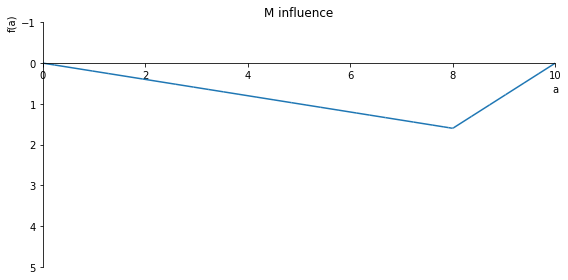
sp.plot(M.subs(x, x_value), ylim=(5, -1), xlim=(0, 10), size=(8, 4), title='M influence')
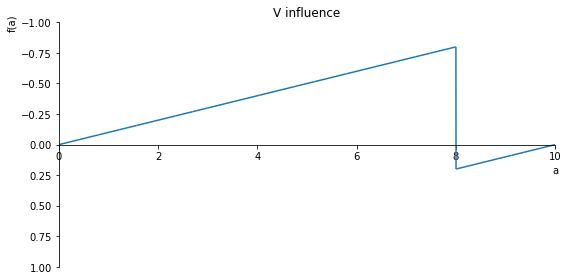
sp.plot(V.subs(x, x_value), ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='V influence')

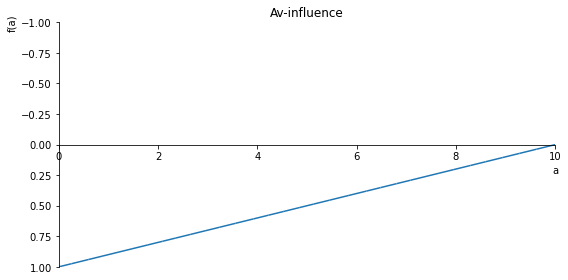
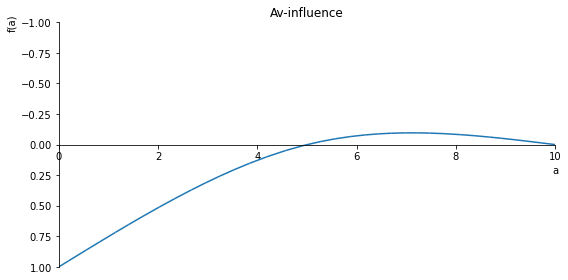
Av_inlfuence = (1/10)*sf(10, a, 1)
sp.plot(Av_inlfuence, ylim=(1, -1), xlim=(0, 10), size=(8, 4), title= 'Av-influence')
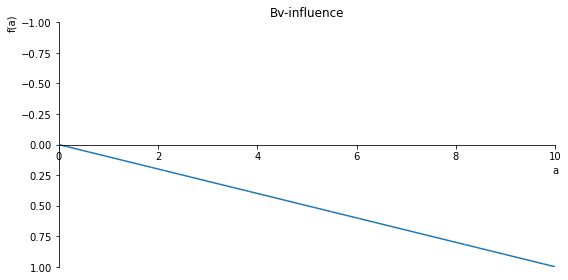
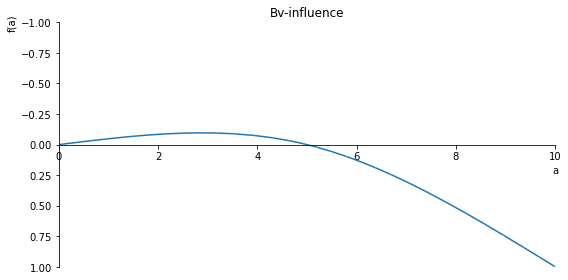
Bv_inlfuence = (1 - (1/10)*sf(10, a, 1))
sp.plot(Bv_inlfuence, ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='Bv-influence')


plt.show()

../../_images/14323f798f0cbc229b59d7687546a209e7379016d2eb0b882ba6e78e83370824.png

../../_images/0d1f926945c037940a8518e1ea17bd478a4623819aab9b20ddea1ce6ace382b5.png

../../_images/1880db01a2e170a601474249e6d5c15078c3bb209f76c111d7b452d918c86936.png

../../_images/de8b6bdbc382c406abdd4278691532fe24ade8b6b2e8d92ca7596e0b060765e6.png

../../_images/9c625248b78fcbe341edc126ee816604bac54c42a696b459a1fa19e52282e9b5.png

../../_images/6a6638479d78144457b7cac73742a68eb056c105918491c0387490aaceca5755.png

../../_images/1cdb07d7ce647aea55767cee3b9736ffa8f47ae14270f06292dab5b712937b15.png

../../_images/3083424b7db223e1caf46b8715e35b0e21a62dc0054f2b26ca37103e65d6dead.png

../../_images/cc5496f1371d3827416ce933f28360f7616be7a41374c17a4eaa59949246d934.png

../../_images/0f1c99d122bce3f8ce0fa030c457fb565d1b82b22edf36a41795cc5707634c7a.png

# voorbeeld 2.
w_influence = (-1/6)*((-sf(5, a, 1) + sf(10, a, 1))/5)*sf(x, 0, 3) + (1/2)*(-2*sf(5, a, 1)+sf(10, a, 1))*sf(x, 0, 2) + 1/6*sf(x, a, 3) + ((20/3)*(-sf(5, a, 1) + sf(10, a, 1)) - 20*(-sf(5, a, 1) + (1/2)*sf(10, a, 1)) - (1/30)*sf(10, a, 3))*sf(x, 5, 1) - (1/6)*(1 - ((-sf(5, a, 1) + sf(10, a, 1))/5))*sf(x, 10, 3)
phi = sp.diff(w_influence, x)*-1
M = sp.diff(phi, x)
V = sp.diff(M, x)

x_value = 8
a_value = 5

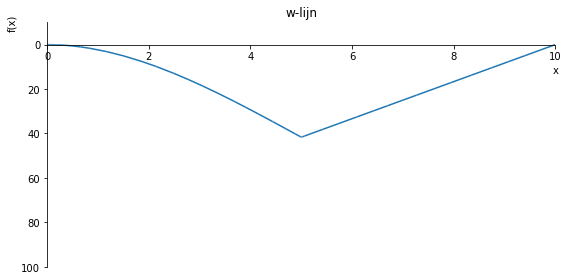
sp.plot(w_influence.subs(a, a_value), ylim=(100, -10), xlim=(0, 10), size=(8, 4), title='w-lijn')
sp.plot(phi.subs(a, a_value), ylim=(30, -30), xlim=(0, 10), size=(8, 4), title='phi-lijn')
sp.plot(M.subs(a, a_value), ylim=(5, -10), xlim=(0, 10), size=(8, 4), title='M-lijn')
sp.plot(V.subs(a, a_value), ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='V-lijn')


sp.plot(w_influence.subs(x, x_value), ylim=(40, -10), xlim=(0, 10), size=(8, 4), title='w-influence')
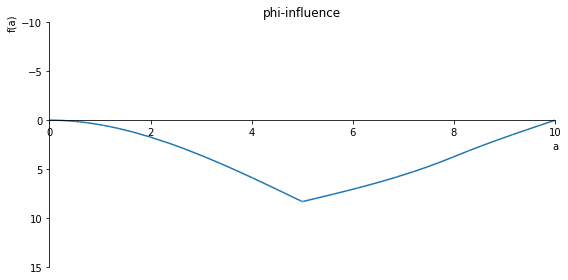
sp.plot(phi.subs(x, x_value), ylim=(15, -10), xlim=(0, 10), size=(8, 4), title='phi-influence')
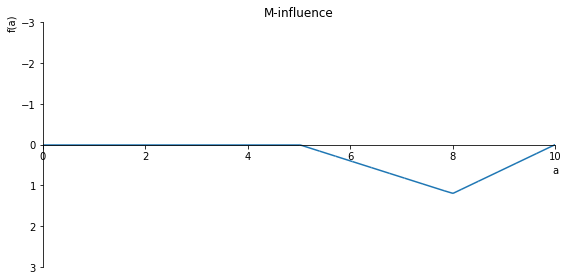
sp.plot(M.subs(x, x_value), ylim=(3, -3), xlim=(0, 10), size=(8, 4), title='M-influence')
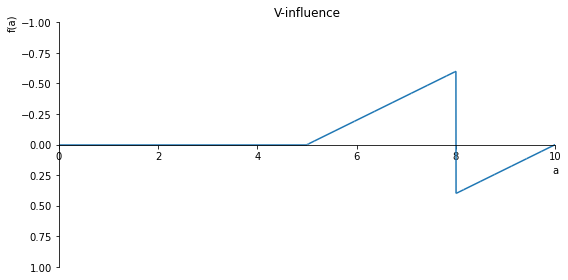
sp.plot(V.subs(x, x_value), ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='V-influence')


Av_inlfuence = (-sf(5, a, 1) + sf(10, a, 1))/5
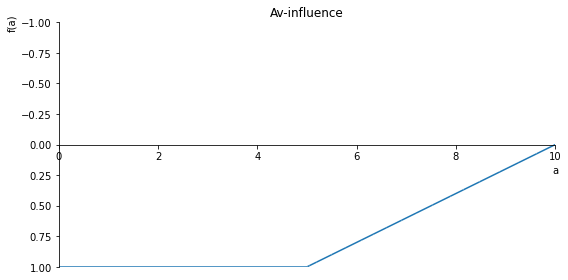
sp.plot(Av_inlfuence, ylim=(1, -1), xlim=(0, 10), size=(8, 4), title= 'Av-influence')
Bv_inlfuence = 1- (-sf(5, a, 1) + sf(10, a, 1))/5
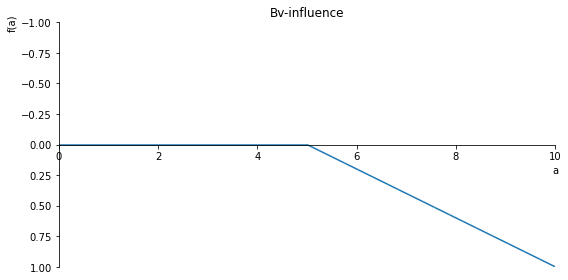
sp.plot(Bv_inlfuence, ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='Bv-influence')
Am = -2*sf(5, a, 1) + sf(10, a, 1)
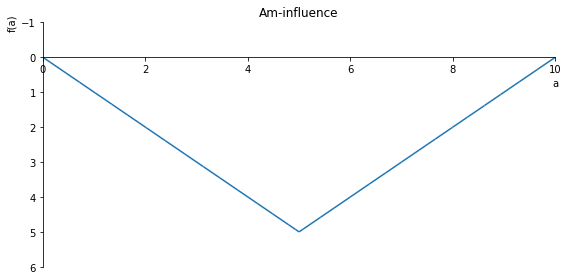
sp.plot(Am, ylim=(6, -1), xlim=(0, 10), size=(8, 4), title='Am-influence')



plt.show()

../../_images/1875e8b589b97f987103163b596d360109a45039806eaca64a462cf12fe69aea.png

../../_images/16217d28aa73ee9a73496be095448facced346d531953aa211f2e915e2a68b9b.png

../../_images/026587548821b7af9955635263404503aab731bab8a9ba342ffaaac0596c410a.png

../../_images/91ff6e9b55c768c5c0d6686018c45b9d682856715b0e082f79c18de45510d568.png

../../_images/a86b0513129a74c7a2b08701bae662fcfa4a1abf892dfe93e4f29c2033ee4cd7.png

../../_images/3e93cd2a4e26a52fe0e0009838793310b300412c17a0e66c6c37c21d862a599f.png

../../_images/fc2861f9210faf1320744e2e2c85e2633bd6798d420e83804dda23b6b2be5855.png

../../_images/066fda2916d00d8329002d9fc57562524792aafcb77592852c2a0028eeff02fd.png

../../_images/02de1f485147a23a4cbd1e3ae23c312e71ca2d85316b403d99388ad94e92d899.png

../../_images/0b9cd60ec49aa456bb67d6a3145897d5fd8608c51e1fa7aeb81987599f3b5a49.png

../../_images/dd7a6a6275c9b3736f4dc7357ae17a9e64ed5d3f2846e700037b80ae1573835e.png

# voorbeeld 3
Av_influence = (sf(10, a, 2) - sf(4, a, 2))/20
Bv_influence = sf(10, a, 1) - sf(4, a, 1) - ((sf(10, a, 2) - sf(4, a, 2))/20)
C_phi = -(5/6)*(sf(10, a, 2) - sf(4, a, 2)) + (1/240)*sf(10, a, 4) - (1/240)*sf(4, a, 4)


w_influence = (-1/6)*((sf(10, a, 2) - sf(4, a, 2))/20)*sf(x, 0, 3) + 1/24*sf(x, a, 4) - 1/24*sf(x, a+6, 4) - (1/6)*(sf(10, a, 1) - sf(4, a, 1)- ((sf(10, a, 2) - sf(4, a, 2))/20))*sf(x, 10, 3) - (-(5/6)*(sf(10, a, 2) - sf(4, a, 2)) + (1/240)*sf(10, a, 4) - (1/240)*sf(4, a, 4))*x
phi = sp.diff(w_influence, x)*-1
M = sp.diff(phi, x)
V = sp.diff(M, x)

x_value = 8
a_value = 2

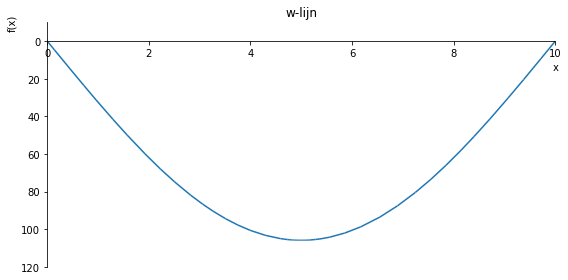
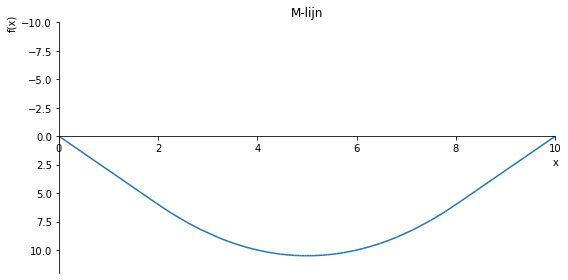
sp.plot(w_influence.subs(a, a_value), ylim=(120, -10), xlim=(0, 10), size=(8, 4), title='w-lijn')
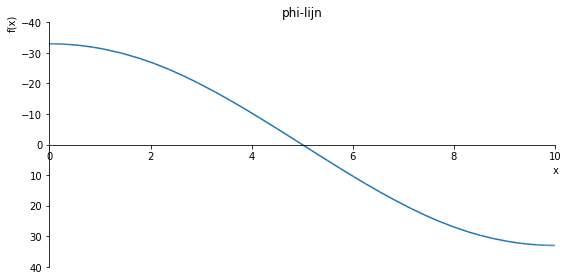
sp.plot(phi.subs(a, a_value), ylim=(40, -40), xlim=(0, 10), size=(8, 4), title='phi-lijn')
sp.plot(M.subs(a, a_value), ylim=(12, -10), xlim=(0, 10), size=(8, 4), title='M-lijn')
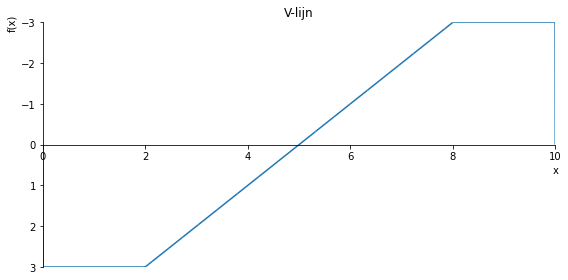
sp.plot(V.subs(a, a_value), ylim=(3, -3), xlim=(0, 10), size=(8, 4), title='V-lijn')


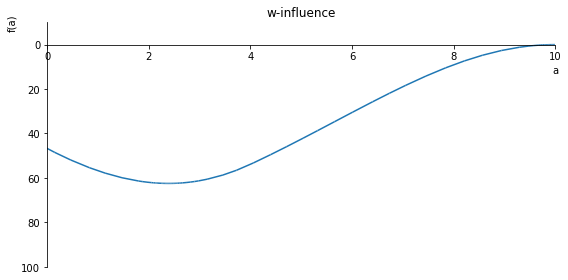
sp.plot(w_influence.subs(x, x_value), ylim=(100, -10), xlim=(0, 10), size=(8, 4), title='w-influence')
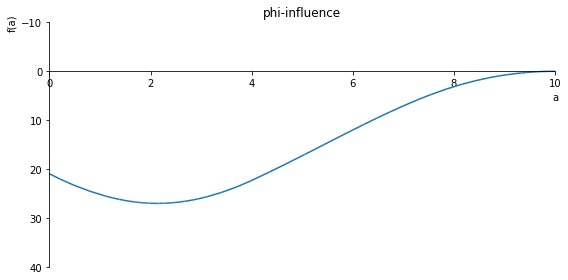
sp.plot(phi.subs(x, x_value), ylim=(40, -10), xlim=(0, 10), size=(8, 4), title='phi-influence')
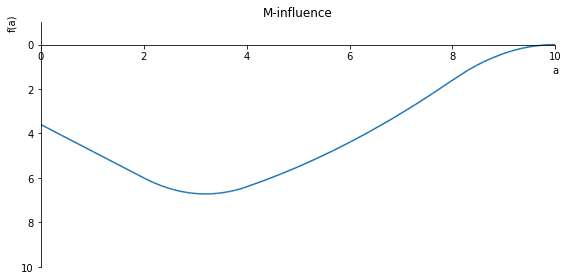
sp.plot(M.subs(x, x_value), ylim=(10, -1), xlim=(0, 10), size=(8, 4), title='M-influence')
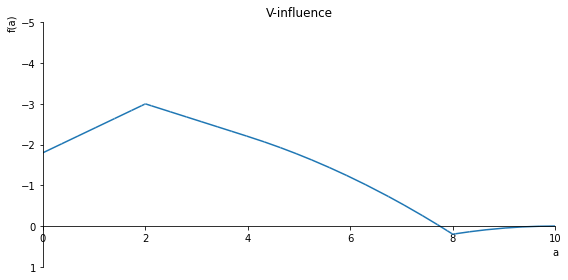
sp.plot(V.subs(x, x_value), ylim=(1, -5), xlim=(0, 10), size=(8, 4), title='V-influence')

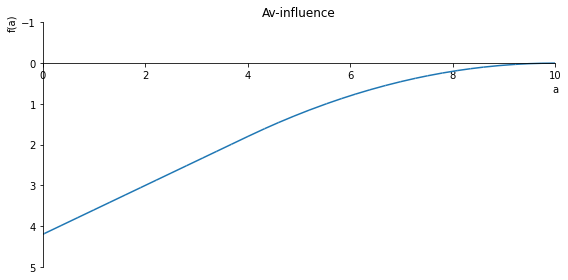
sp.plot(Av_influence, ylim=(5, -1), xlim=(0, 10), size=(8, 4), title='Av-influence')
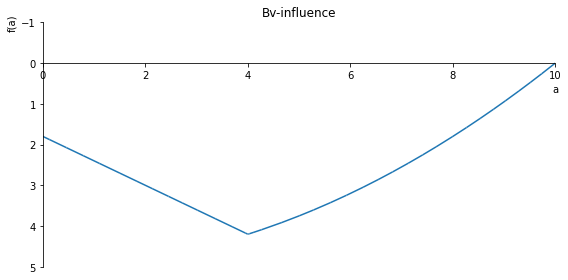
sp.plot(Bv_influence, ylim=(5, -1), xlim=(0, 10), size=(8, 4), title='Bv-influence')

plt.show()

../../_images/8382305d693a5a6e9f46767a4371d323d7cc0758ed348606fc3c4973942b9a52.png

../../_images/c91452785c42880947dc8adb3c78e09fc0efbdbf920510b5b720927e6781b25b.png

../../_images/1c54ca439773b78e72303b7457f6aa74bbdfe51e6cb6a17c88840aa35257ca46.png

../../_images/a37f2e5b2e58bc7f98e7bea55c96a5f85cf00bbfb478c176888f05e0968f15aa.png

../../_images/340e881bf67bf563daa648164b7c5c4417ced7fb6bad5a15b227800939092dd0.png

../../_images/84fda063f796162def591c8393c1f0785a2661aa99b41141cac23ecdf865f644.png

../../_images/a1fee6db3c5d28a22d60f07725f31d6615372408f5c2f84c8959378eb2066d2c.png

../../_images/51bd3ca7ef50070e49fe3659808901d23e9b961e13064019913427c420b8f59b.png

../../_images/56b5cf754c64f5e12c193e632ccf5706a550d50b0d3ec46272461ff77af523b4.png

../../_images/5997436abc6cc3776fcf176d113b3e0a1f02c4b5666745a48a7fe0d005c33862.png

# voorbeeld 4
Av_influence = (1/500)*sf(10, a, 3) - (1/20)*sf(10, a, 1) - (1/250)*sf(5, a, 3)
Cv_influence = -2*(Av_influence) + (1/5)*sf(10, a, 1)
Bv_influence = 1 - Av_influence - Cv_influence
Cphi = -(25/6)*Av_influence +(1/30)*sf(5, a, 3)

w_influence = (-1/6)*(Av_influence)*sf(x, 0, 3) + (1/6)*sf(x, a, 3) - (1/6)*Cv_influence*sf(x, 5, 3) - (1/6)*Bv_influence*sf(x, 10, 3) - Cphi*x
phi = sp.diff(w_influence, x)*-1
M = sp.diff(phi, x)
V = sp.diff(M, x)

x_value = 4
a_value = 2

sp.plot(w_influence.subs(a, a_value), ylim=(2, -1), xlim=(0, 10), size=(8, 4), title='w-lijn')
sp.plot(phi.subs(a, a_value), ylim=(2, -2), xlim=(0, 10), size=(8, 4), title='phi-lijn')
sp.plot(M.subs(a, a_value), ylim=(2, -2), xlim=(0, 10), size=(8, 4), title='M-lijn')
sp.plot(V.subs(a, a_value), ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='V-lijn')


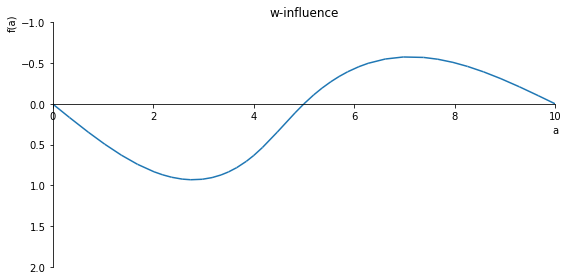
sp.plot(w_influence.subs(x, x_value), ylim=(2, -1), xlim=(0, 10), size=(8, 4), title='w-influence')
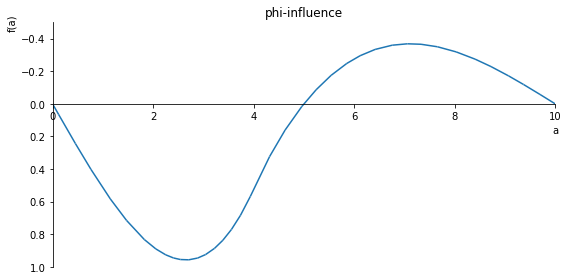
sp.plot(phi.subs(x, x_value), ylim=(1, -(1/2)), xlim=(0, 10), size=(8, 4), title='phi-influence')
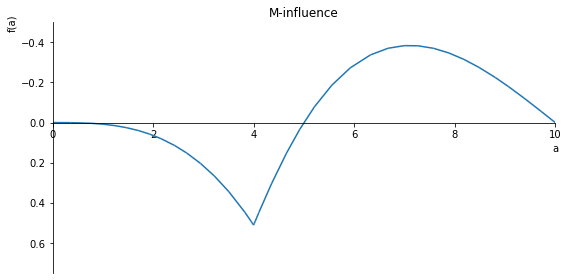
sp.plot(M.subs(x, x_value), ylim=(0.75, -0.5), xlim=(0, 10), size=(8, 4), title='M-influence')
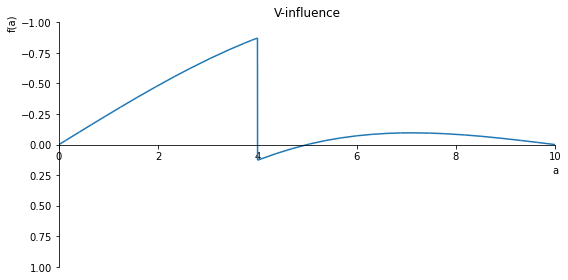
sp.plot(V.subs(x, x_value), ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='V-influence')


sp.plot(Av_influence, ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='Av-influence')
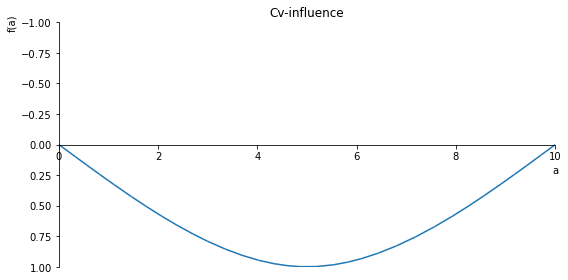
sp.plot(Cv_influence, ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='Cv-influence')
sp.plot(Bv_influence, ylim=(1, -1), xlim=(0, 10), size=(8, 4), title='Bv-influence')



plt.show()

../../_images/a2e10c154dccd64406cac4f0e1ca6b4c9f07442b72f57f00e5b366d62f62ab5d.png

../../_images/d540fea151fc777e8db3ffbf93ef62b273e48ceb035579d252aae3de9238bcfe.png

../../_images/649c7a1432b9d8551b66a288e48a7d944a0bb5e6fd4bbb5aadfcdf7d3d8a4926.png

../../_images/13f46fb4642018904237666f85a15c69dac5a0af14a547e98b27275f89f05a77.png

../../_images/7d87bd15d27ac3bc24d51fecd7d1c103be313e150b743835993cf61c960fcda8.png

../../_images/ac897b36e3294134460bdc51982c71ad81efb02290340a9e178ad5c9c7b9f048.png

../../_images/0f532608d347115950d563320ad7fb15546d89d47fdd38cdd8ad07202b03ea07.png

../../_images/0fe714d0fbd1869137afd07ef835866f52af8e47480e6fad9900a7c174d4973a.png

../../_images/4259aea9cba7b119eda7131fb7433515d93a54f263e223311a8ffc530638e2d5.png

../../_images/58edf52dad46a14d5bc32429fbb3e56a614a1d04aeb6e55e184bbec11842e557.png

../../_images/84c9978163115ff6b634309a2d86b810ab3b6809224379b4358fe8c87a2d5aa0.png

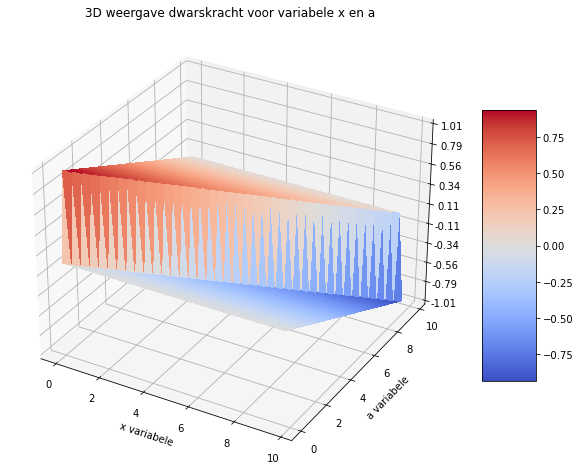
# 3D plotje

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from matplotlib.ticker import LinearLocator
import sympy as sp
sf = sp.SingularityFunction

fig = plt.figure(figsize=(10, 10))
ax = fig.gca(projection='3d')

x = np.arange(0, 10, 0.25)
a = np.arange(0, 10, 0.25)
X, A = np.meshgrid(x, a)

def V(x, a):
    sf_x = np.where(x >= 0, 1, 0)
    sf_xa = np.where(x - a >= 0, 1, 0)
    sf_x10 = np.where(x - 10 >= 0, 1, 0)
    return ((10-a)/10)*1.0*sf_x - 1.0*sf_xa + (a/10)*1.0*sf_x10

Z = V(X, A)

surf = ax.plot_surface(X, A, Z, cmap=cm.coolwarm, linewidth=0, antialiased=False)
ax.set_zlim(-1.01, 1.01)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter('{x:.02f}')

fig.colorbar(surf, shrink=0.5, aspect=5)

plt.xlabel('x variabele')
plt.ylabel('a variabele')
plt.title('3D weergave dwarskracht voor variabele x en a')
plt.show()

../../_images/ec51549061382957d4b4ab26fa74b04b93d10b954f73af7782db16282cc24371.png