Alex: Twodimensional structures

Contents

Alex: Twodimensional structures#

In dit rapport wordt uitgelegd hoe de Macaulay methode kan worden uitgebreid zodat het toepasbaar is op geknikte, vertakte en gesloten constructies, inclusief gescharnierde. Het model is robuust, systematisch toepasbaar, kan de snedekrachten en globale verplaatsingen op elk punt berekenen en de oplossingsvoorwaarden zijn eenvoudiger en geringer in aantal in vergelijking met de directe integratie methode.

Het model maakt gebruik van een globaal en een lokaal assenstelsel (\((h,v)\) en \((x,z)\)). In figuur 1 wordt het verloop van het lokaal assenstelsel aangegeven met de nummering van de blauwe pijlen. De belastingen en de verplaatsingen worden globaal genoteerd en de snedekrachtdiagrammen lokaal. Er zijn twee vergelijkingen die de lokale as volgen. \(q_{z}(x)\) is voor de krachten loodrecht op de staaf en integreert naar de dwarskrachtenvergelijking, enz. en \(q_{x}(x)\) is voor de krachten parallel aan de staaf en integreert naar de normaalkrachtenvergelijking, enz.

De belastingen worden in 2D anders gemodelleerd dan in 1D. Er wordt in het model onderscheid gemaakt tussen een koppel (\(T\)), verticale en horizontale puntlast (\(F_{v}\) en \(F_{h}\)), verticale en horizontale gelijkmatig verdeelde belasting (\(q_{v}\) en \(q_{h}\)) en scharnier (\(EI\varphi_{s}\)). De vergelijking voor elke belasting is anders voor \(q_{z}(x)\) en \(q_{x}(x)\) en bestaan telkens uit een beginterm (\(b\)) voor het aangrijppunt van de belasting en een systematische reeks hoektermen (\(a_{i}\)) voor elke hoek (\(\theta_{i}\)) waar de functie van \(x\) langs gaat na het aangrijppunt van de belasting. De vergelijkingen zijn als volgt:

koppel

\[q_{z}(x) = T\left\langle x - b \right\rangle^{- 2}\]
\[q_{x}(x) = 0\]

Verticale Puntlast

\[q_{z}(x) = F_{v}\left( \left\langle x - b \right\rangle^{- 1}\cos\left( \theta_{b} \right) + \sum_{}^{}\left( \left\langle x - a_{i} \right\rangle^{- 1}\left( \cos\left( \theta_{i} \right) - \cos\left( \theta_{i - 1} \right) \right) \right) \right)\ ;\ \ voor\ a_{i} > b\]
\[q_{x}(x) = - F_{v}\left( \left\langle x - b \right\rangle^{- 1}\sin\left( \theta_{b} \right) + \sum_{}^{}\left( \left\langle x - a_{i} \right\rangle^{- 1}\left( \sin\left( \theta_{i} \right) - \sin\left( \theta_{i - 1} \right) \right) \right) \right)\ ;\ \ voor\ a_{i} > b\]

Horizontale puntlast

\[q_{z}(x) = F_{h}\left( \left\langle x - b \right\rangle^{- 1}\sin\left( \theta_{b} \right) + \sum_{}^{}\left( \left\langle x - a_{i} \right\rangle^{- 1}\left( \sin\left( \theta_{i} \right) - \sin\left( \theta_{i - 1} \right) \right) \right) \right)\ ;\ \ voor\ a_{i} > b\]
\[q_{x}(x) = F_{h}\left( \left\langle x - b \right\rangle^{- 1}\cos\left( \theta_{b} \right) + \sum_{}^{}\left( \left\langle x - a_{i} \right\rangle^{- 1}\left( \cos\left( \theta_{i} \right) - \cos\left( \theta_{i - 1} \right) \right) \right) \right)\ ;\ \ voor\ a_{i} > b\]

Verticale Gelijkmatig Verdeelde Belasting

\[\begin{split}q_{z}(x) = q_{v}\begin{pmatrix} \left\langle x - b \right\rangle^{0}\cos\left( \theta_{b} \right) + \\ \sum_{}^{}\left( \left( {(\left\langle x - a_{i} \right\rangle}^{0} + \left\langle x - a_{i} \right\rangle^{- 1}\left( a_{i} - b \right) \right)\left( \cos\left( \theta_{i} \right) - \cos\left( \theta_{i - 1} \right) \right) \right) \\ \end{pmatrix}\ \ ;\ \ voor\ a_{i} > b\end{split}\]
\[\begin{split}q_{x}(x) = - q_{v}\begin{pmatrix} \left\langle x - b \right\rangle^{0}\sin\left( \theta_{b} \right) + \\ \sum_{}^{}\left( \left( {(\left\langle x - a_{i} \right\rangle}^{0} + \left\langle x - a_{i} \right\rangle^{- 1}\left( a_{i} - b \right) \right)\left( \sin\left( \theta_{i} \right) - \sin\left( \theta_{i - 1} \right) \right) \right) \\ \end{pmatrix}\ \ ;\ \ voor\ a_{i} > b\end{split}\]

Horizontaal Gelijkmatig Verdeelde Belasting

\[\begin{split}q_{z}(x) = q_{h}\begin{pmatrix} \left\langle x - b \right\rangle^{0}\sin\left( \theta_{b} \right) + \\ \sum_{}^{}\left( \left( {(\left\langle x - a_{i} \right\rangle}^{0} + \left\langle x - a_{i} \right\rangle^{- 1}\left( a_{i} - b \right) \right)\left( \sin\left( \theta_{i} \right) - \sin\left( \theta_{i - 1} \right) \right) \right) \\ \end{pmatrix}\ \ ;\ \ voor\ a_{i} > b\end{split}\]
\[\begin{split}q_{x}(x) = q_{h}\begin{pmatrix} \left\langle x - b \right\rangle^{0}\cos\left( \theta_{b} \right) + \\ \sum_{}^{}\left( \left( {(\left\langle x - a_{i} \right\rangle}^{0} + \left\langle x - a_{i} \right\rangle^{- 1}\left( a_{i} - b \right) \right)\left( \cos\left( \theta_{i} \right) - \cos\left( \theta_{i - 1} \right) \right) \right) \\ \end{pmatrix}\ \ ;\ \ voor\ a_{i} > b\end{split}\]

Scharnier

\[q_{z}(x) = EI\varphi_{s}\left\langle x - b \right\rangle^{- 3}\]
\[q_{x}(x) = 0\]

De doorbuiging (\(u_{z}(x)\)) en extensie (\(u_{x}(x)\)) zijn voor tweedimensionale constructies hele abstracte termen die niet bruikbaar zijn voor de oplossingsvoorwaarden. Daarom moeten ze worden gebruikt als invoer voor de vergelijkingen van de horizontale en verticale verplaatsing van de constructie (\(u_{h}(x)\) en \(u_{v}(x)\)). Deze vergelijkingen zijn als volgt:

\[\begin{split}u_{v}(x) = u_{z}\left( a_{0} \right)\cos\left( \theta_{0} \right) - u_{x}\left( a_{0} \right)\sin\left( \theta_{0} \right) + \sum_{i = 0}^{i = n}\begin{pmatrix} \left( \left( u_{z}(x) - u_{z}\left( a_{i} \right) \right)\left\langle x - a_{i} \right\rangle^{0} - \left( u_{z}(x) - u_{z}\left( a_{j} \right) \right)\left\langle x - a_{j} \right\rangle^{0} \right)\cos\left( \theta_{i} \right) \\ - \left( \left( u_{x}(x) - u_{x}\left( a_{i} \right) \right)\left\langle x - a_{i} \right\rangle^{0} - \left( u_{x}(x) - u_{x}\left( a_{j} \right) \right)\left\langle x - a_{j} \right\rangle^{0} \right)\sin\left( \theta_{i} \right) \\ \end{pmatrix}\end{split}\]
\[\begin{split}u_{h}(x) = u_{z}\left( a_{0} \right)\sin\left( \theta_{0} \right) + u_{x}\left( a_{0} \right)\cos\left( \theta_{0} \right) + \sum_{i = 0}^{i = n}\begin{matrix} \begin{pmatrix} \left( \left( u_{z}(x) - u_{z}\left( a_{i} \right) \right)\left\langle x - a_{i} \right\rangle^{0} - \left( u_{z}(x) - u_{z}\left( a_{j} \right) \right)\left\langle x - a_{j} \right\rangle^{0} \right)\sin\left( \theta_{i} \right) \\ + \left( \left( u_{x}(x) - u_{x}\left( a_{i} \right) \right)\left\langle x - a_{i} \right\rangle^{0} - \left( u_{x}(x) - u_{x}\left( a_{j} \right) \right)\left\langle x - a_{j} \right\rangle^{0} \right)\cos\left( \theta_{i} \right) \\ \end{pmatrix} \\ \end{matrix}\end{split}\]

Hierbij is \(a_{i}\) het beginpunt, \(a_{j}\) het eindpunt en \(\theta_{i}\) de hoek van staaf \(ij\).

Voor vertakte en gesloten constructies bestaan er drie bijzondere punten met unieke eigenschappen. Dit zijn het knooppunt (\(a_{k}\)), sprongpunt (\(a_{s}\)) en aansluitpunt (\(a_{a}\)).

Het knooppunt is het punt waarbij de functie van \(x\) voor het eerst langs een knoop gaat. Op \(a_{k}\) moet voor elke staaf \(IJ\) waarnaar de functie niet direct de weg vervolgd drie onbekende krachten worden toegevoegd \(V^{IJ}\), \(H^{IJ}\) en \(T^{IJ}\). Hierin vertegenwoordigd \(V^{IJ}\) de verticale kracht, \(H^{IJ}\) de horizontale kracht en \(T^{IJ}\) de koppel voortkomend uit staaf \(IJ\) werkend op knoop \(I\).

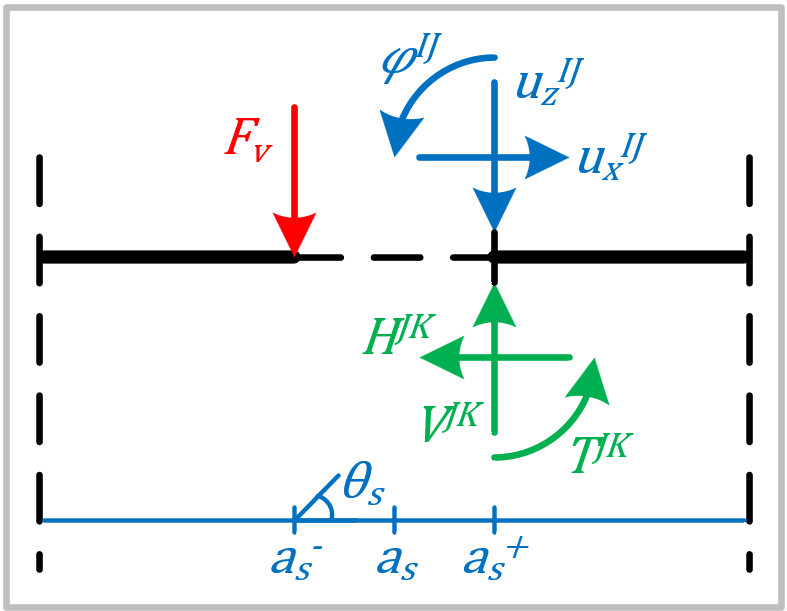
Het sprongpunt, (zie figuur 1) is het punt waar de functie van \(x\) in het globale assenstelsel een sprong maakt van punt \(I\), wat een uiteinde of afsluiting is van een vertakking, naar punt \(J\), wat een knoopverbinding is waar de functie van \(x\) al eerder langs is geweest. Belastingen werkende op punt \(I\) moeten gemodelleerd worden op \(a_{s}^{-}\) en op punt \(J\) op \(a_{s}^{+}\). Op \(a_{s}^{+}\) moeten ook de onbekende krachten \(- V^{JK}\), \(- H^{JK}\) en \(- T^{JK}\) worden toegevoegd voor staaf \(JK\) waarnaar de functie na de sprong de weg vervolgd. Verder moeten op \(a_{s}^{+}\) de sprongconstanten \(\varphi^{IJ}\), \(u_{z}^{IJ}\) en \(u_{x}^{IJ}\) toegevoegd worden voor de sprong in vervormingen tussen punt \(I\) en \(J\). Deze worden als volgt gemodelleerd:

\[q_{z}(x) = EI\varphi^{ij}\left\langle x - a_{s}^{+} \right\rangle^{- 3} + EIu_{z}^{ij}\left\langle x - a_{s}^{+} \right\rangle^{- 4}\]
\[q_{x}(x) = EAu_{x}^{ij}\left\langle x - a_{s}^{+} \right\rangle^{- 2}\]

Afbeelding met tekst, lijn, Lettertype, diagram Automatischgegenereerdebeschrijving

figuur 1: modelleren van een sprongpunt.

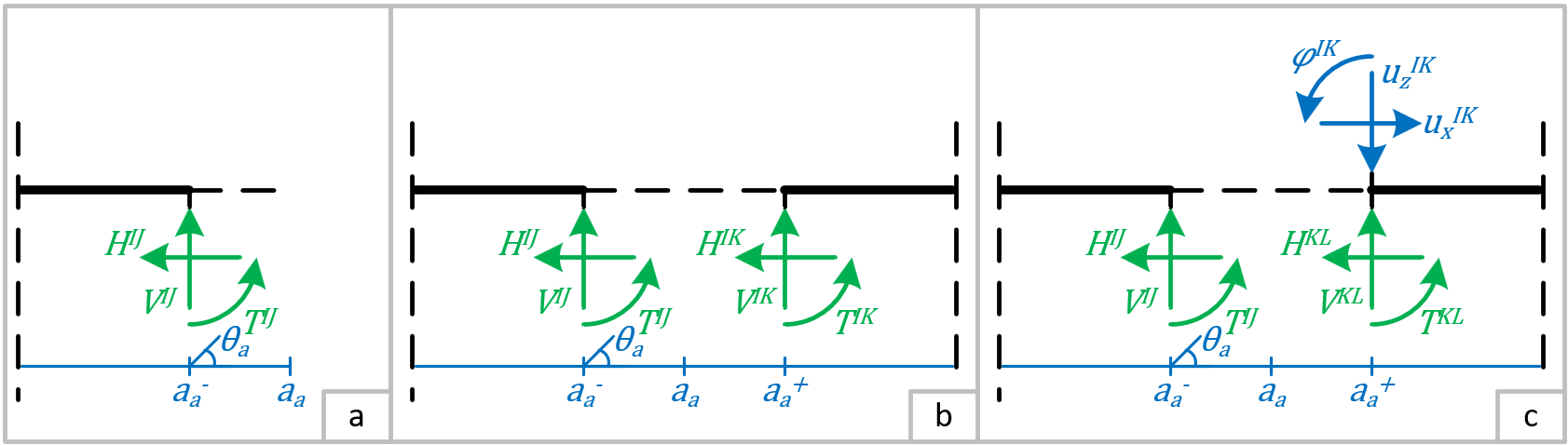
Het aansluitpunt is het punt waarbij de functie van \(x\) opnieuw langs een knoop gaat. Op \(a_{a}^{-}\) moeten de drie onbekende krachten \(- V^{IJ}\), \({- H}^{IJ}\) en \(- T^{IJ}\) voor de staaf \(IJ\) dat aansluit op punt \(I\). Het aansluitpunt kan het einde zijn van de functie, maar de functie kan ook direct de weg vervolgen of een sprong maken. Het verschil in modelleren is te zien in figuur 2.

Afbeelding met lijn, diagram, Perceel, tekst Automatisch gegenereerdebeschrijving

figuur 2: Modelleren van een aansluitpunt als het ook het eindpunt is (a), als de functie erna direct vervolgd (b) of het als het ook een sprongpunt is (c).

In Tabel 1 wordt voorgeschreven welke oplossingsvoorwaarden gelden voor starre tweedimensionale constructies als lokale afstand \(a_{i}\) de benoemde eigenschap heeft. Afstand \(a_{i}\) kan meerdere eigenschappen tegelijk hebben. Hierbij is \(a_{k}\) het knooppunt waarbij de functie voor het eerst langs dezelfde knoop komt als afstand \(a_{i}\) of \(a_{i}^{+}\).

Tabel 1: Oplossingsvoorwaarden voor tweedimensionale starre constructies.

Situatie op \(a_i\)

Oplossingsvoorwaarden

Lokaal beginpunt

\(N\left(a_i^-\right) = 0\)
\(V\left(a_i^-\right) = 0\)
\(M\left(a_i^-\right) = 0\)

Lokaal eindpunt

\(N\left(a_i\right) = 0\)
\(V\left(a_i\right) = 0\)
\(M\left(a_i\right) = 0\)

Globaal eindpunt / sprongpunt (vertakte constructie)

Zie lokaal eindpunt +
\(\varphi\left( a_i^+ \right) - \varphi \left( a_k \right) = 0\)
\(u_v\left( a_i^+ \right) - u_v \left( a_k \right) = 0\)
\(u_h\left( a_i^+ \right) - u_h \left( a_k \right)=0\)

Aansluitpunt (gesloten constructie)

Zie lokaal eindpunt
\(\varphi\left( a_i \right) - \varphi \left( a_k \right) = 0\)
\(u_v\left( a_i \right) - u_v \left( a_k \right) = 0\)
\( u_h\left( a_i \right) - u_h \left( a_j \right) = 0\)

Scharnierverbinding

\(M \left(a_i^+\right) = 0\)

Verticale roloplegging

\(u_v \left(a_i\right) = 0\)

Horizontale roloplegging

\(u_h \left(a_i \right) = 0\)

Scharnierende oplegging

\(u_v \left(a_i\right) = 0\)
\(u_h \left(a_i\right) = 0\)

Inklemming

\(\varphi \left( a_i \right) = 0\)
\(u_v \left(a_i\right) = 0\)
\(u_h \left(a_i\right) = 0\)

Een staaf \(JK\) kan ook scharnierend verbonden zijn aan een knoop. Het modelleren ervan verschilt voor een knoop-, sprong en aansluitpunt. In Tabel 2 staat een overzicht van welke onbekenden en voorwaarden moeten worden toegevoegd en/of wegelaten voor elke situatie t.o.v. een star verbonden staaf. Als alle staven scharnieren verbonden zijn in de knoop, dan moet voor \(n\) staven \(n - 1\) staven een scharnierverbinding worden gemodelleerd in de knoop.

Baudoin [Bau24]

Documenten#

Contents