Example 6#
import sympy as sym
import numpy as np
import matplotlib.pyplot as plt
# algemene gegevens
x = sym.symbols('x')
EI, EA = sym.symbols('EI EA')
CV, CM, Cphi, Cuz, CN, Cux = sym.symbols('C_V C_M C_phi C_uz C_N C_ux')
dx = 2*10**-15
# gegevens constructie
a0, a1, a2, a3, a4, a5, a6 = 0, 2, 6, 7, 11, 12, 14
aa = [a0, a1, a2, a3, a4, a5, a6]
o0, o1, o2, o3, o4, o5 = 0, 0, -sym.pi/2, sym.pi, sym.pi/2, 0
oo = [o0, o1, o2, o3, o4, o5]
# sprongen in de x functie
phiBC, uzBC, uxBC = sym.symbols('phi^BC u_z^BC u_x^BC')
s1 = 12+2*dx
ss = [s1]
# gegevens belastingen
Fv, qv = 50, 10
RvA, RhA, RvF = sym.symbols('R_v^A R_h^A R_v^F')
VBE, HBE, TBE, VCD, HCD, TCD = sym.symbols('V^BE H^BE T^BE V^CD H^CD T^CD')
B = [RvA, RhA, qv, -qv, VBE, HBE, TBE, Fv, VCD, HCD, TCD, -VBE, -HBE, -TBE, -VCD, -HCD, -TCD, phiBC, uzBC, uxBC, qv, RvF]
b1, b2, b3, b4, b5, b6, b7 = 0, 2, 4, 6, 12, 12+2*dx, 14
bb = [b1, b1, b1, b4, b2, b2, b2, b3, b4, b4, b4, b5, b5, b5, b6, b6, b6, b6, b6, b6, b6, b7]
# K = 1, Fv = 2, Fh = 3, qv = 4, qh = 5, phi = 6, uz = 7, ux = 8
nn = [2, 3, 4, 4, 2, 3, 1, 2, 2, 3, 1, 2, 3, 1, 2, 3, 1, 6, 7, 8, 4, 2]
#qz opstellen
qz = 0
#beginpunten
for i in range(len(B)):
for j in range(len(aa)):
if bb[i] == aa[-1]:
if nn[i] == 1:
qz += B[i] * sym.SingularityFunction(x,bb[i],-2)
if nn[i] == 2:
qz += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.cos(oo[-1])
if nn[i] == 3:
qz += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.sin(oo[-1])
if nn[i] == 4:
qz += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.cos(oo[-1])
if nn[i] == 5:
qz += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.sin(oo[-1])
break
else:
if bb[i] < aa[j]:
if nn[i] == 1:
qz += B[i] * sym.SingularityFunction(x,bb[i],-2)
if nn[i] == 2:
qz += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.cos(oo[j-1])
if nn[i] == 3:
qz += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.sin(oo[j-1])
if nn[i] == 4:
qz += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.cos(oo[j-1])
if nn[i] == 5:
qz += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.sin(oo[j-1])
if nn[i] == 6:
qz += B[i] * sym.SingularityFunction(x,bb[i],-3) * EI
if nn[i] == 6:
qz += B[i] * sym.SingularityFunction(x,bb[i],-3) * EI
if nn[i] == 7:
qz += B[i] * sym.SingularityFunction(x,bb[i],-4) * EI
break
# knikpunten
for i in range(len(B)):
for j in range(len(aa)-1):
if bb[i] < aa[j]:
if nn[i] == 2:
qz += B[i] * sym.SingularityFunction(x,aa[j],-1) * (sym.cos(oo[j]) - sym.cos(oo[j-1]))
if nn[i] == 3:
qz += B[i] * sym.SingularityFunction(x,aa[j],-1) * (sym.sin(oo[j]) - sym.sin(oo[j-1]))
if nn[i] == 4:
qz += B[i] * ((sym.SingularityFunction(x,aa[j],0) + sym.SingularityFunction(x,aa[j],-1) * (aa[j] - bb[i])) * (sym.cos(oo[j]) - sym.cos(oo[j-1])))
if nn[i] == 5:
qz += B[i] * ((sym.SingularityFunction(x,aa[j],0) + sym.SingularityFunction(x,aa[j],-1) * (aa[j] - bb[i])) * (sym.sin(oo[j]) - sym.sin(oo[j-1])))
display(qz)
\[\displaystyle 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{-3} + EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{-4} - H^{BE} {\left\langle x - 6 \right\rangle}^{-1} + H^{BE} {\left\langle x - 7 \right\rangle}^{-1} + H^{BE} {\left\langle x - 11 \right\rangle}^{-1} - H^{BE} {\left\langle x - 12 \right\rangle}^{-1} - H^{CD} {\left\langle x - 6 \right\rangle}^{-1} + H^{CD} {\left\langle x - 7 \right\rangle}^{-1} + H^{CD} {\left\langle x - 11 \right\rangle}^{-1} - H^{CD} {\left\langle x - 12 \right\rangle}^{-1} - R^{A}_{h} {\left\langle x - 6 \right\rangle}^{-1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{-1} + R^{A}_{h} {\left\langle x - 11 \right\rangle}^{-1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{-1} + R^{A}_{v} {\left\langle x \right\rangle}^{-1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{-1} - R^{A}_{v} {\left\langle x - 7 \right\rangle}^{-1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{-1} + R^{A}_{v} {\left\langle x - 12 \right\rangle}^{-1} + R^{F}_{v} {\left\langle x - 14 \right\rangle}^{-1} + T^{BE} {\left\langle x - 2 \right\rangle}^{-2} - T^{BE} {\left\langle x - 12 \right\rangle}^{-2} + T^{CD} {\left\langle x - 6 \right\rangle}^{-2} - T^{CD} {\left\langle x - 12.0 \right\rangle}^{-2} + V^{BE} {\left\langle x - 2 \right\rangle}^{-1} - V^{BE} {\left\langle x - 6 \right\rangle}^{-1} - V^{BE} {\left\langle x - 7 \right\rangle}^{-1} + V^{BE} {\left\langle x - 11 \right\rangle}^{-1} - V^{CD} {\left\langle x - 7 \right\rangle}^{-1} + V^{CD} {\left\langle x - 11 \right\rangle}^{-1} + V^{CD} {\left\langle x - 12 \right\rangle}^{-1} - V^{CD} {\left\langle x - 12.0 \right\rangle}^{-1} + 10 {\left\langle x \right\rangle}^{0} + 50 {\left\langle x - 4 \right\rangle}^{-1} - 110 {\left\langle x - 6 \right\rangle}^{-1} - 10 {\left\langle x - 6 \right\rangle}^{0} - 110 {\left\langle x - 7 \right\rangle}^{-1} + 110 {\left\langle x - 11 \right\rangle}^{-1} + 110 {\left\langle x - 12 \right\rangle}^{-1} + 10 {\left\langle x - 12.0 \right\rangle}^{0}\]
#qx opstellen
qx = 0
#beginpunten
for i in range(len(B)):
for j in range(len(aa)):
if bb[i] == aa[-1]:
if nn[i] == 2:
qx += B[i] * sym.SingularityFunction(x,bb[i],-1) * -sym.sin(oo[-1])
if nn[i] == 3:
qx += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.cos(oo[-1])
if nn[i] == 4:
qx += B[i] * sym.SingularityFunction(x,bb[i],0) * -sym.sin(oo[-1])
if nn[i] == 5:
qx += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.cos(oo[-1])
break
else:
if bb[i] < aa[j]:
if nn[i] == 2:
qx += B[i] * sym.SingularityFunction(x,bb[i],-1) * -sym.sin(oo[j-1])
if nn[i] == 3:
qx += B[i] * sym.SingularityFunction(x,bb[i],-1) * sym.cos(oo[j-1])
if nn[i] == 4:
qx += B[i] * sym.SingularityFunction(x,bb[i],0) * -sym.sin(oo[j-1])
if nn[i] == 5:
qx += B[i] * sym.SingularityFunction(x,bb[i],0) * sym.cos(oo[j-1])
if nn[i] == 8:
qx += B[i] * sym.SingularityFunction(x,bb[i],-2) * EA
break
# knikpunten
for i in range(len(B)):
for j in range(len(aa)-1):
if bb[i] < aa[j]:
if nn[i] == 2:
qx += B[i] * sym.SingularityFunction(x,aa[j],-1) * (-sym.sin(oo[j]) + sym.sin(oo[j-1]))
if nn[i] == 3:
qx += B[i] * sym.SingularityFunction(x,aa[j],-1) * (sym.cos(oo[j]) - sym.cos(oo[j-1]))
if nn[i] == 4:
qx += B[i] * ((sym.SingularityFunction(x,aa[j],0) + sym.SingularityFunction(x,aa[j],-1) * (aa[j] - bb[i])) * (-sym.sin(oo[j]) + sym.sin(oo[j-1])))
if nn[i] == 5:
qx += B[i] * ((sym.SingularityFunction(x,aa[j],0) + sym.SingularityFunction(x,aa[j],-1) * (aa[j] - bb[i])) * (sym.cos(oo[j]) - sym.cos(oo[j-1])))
display(qx)
\[\displaystyle EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{-2} + H^{BE} {\left\langle x - 2 \right\rangle}^{-1} - H^{BE} {\left\langle x - 6 \right\rangle}^{-1} - H^{BE} {\left\langle x - 7 \right\rangle}^{-1} + H^{BE} {\left\langle x - 11 \right\rangle}^{-1} - H^{CD} {\left\langle x - 7 \right\rangle}^{-1} + H^{CD} {\left\langle x - 11 \right\rangle}^{-1} + H^{CD} {\left\langle x - 12 \right\rangle}^{-1} - H^{CD} {\left\langle x - 12.0 \right\rangle}^{-1} + R^{A}_{h} {\left\langle x \right\rangle}^{-1} - R^{A}_{h} {\left\langle x - 6 \right\rangle}^{-1} - R^{A}_{h} {\left\langle x - 7 \right\rangle}^{-1} + R^{A}_{h} {\left\langle x - 11 \right\rangle}^{-1} + R^{A}_{h} {\left\langle x - 12 \right\rangle}^{-1} + R^{A}_{v} {\left\langle x - 6 \right\rangle}^{-1} - R^{A}_{v} {\left\langle x - 7 \right\rangle}^{-1} - R^{A}_{v} {\left\langle x - 11 \right\rangle}^{-1} + R^{A}_{v} {\left\langle x - 12 \right\rangle}^{-1} + V^{BE} {\left\langle x - 6 \right\rangle}^{-1} - V^{BE} {\left\langle x - 7 \right\rangle}^{-1} - V^{BE} {\left\langle x - 11 \right\rangle}^{-1} + V^{BE} {\left\langle x - 12 \right\rangle}^{-1} + V^{CD} {\left\langle x - 6 \right\rangle}^{-1} - V^{CD} {\left\langle x - 7 \right\rangle}^{-1} - V^{CD} {\left\langle x - 11 \right\rangle}^{-1} + V^{CD} {\left\langle x - 12 \right\rangle}^{-1} + 110 {\left\langle x - 6 \right\rangle}^{-1} - 110 {\left\langle x - 7 \right\rangle}^{-1} - 110 {\left\langle x - 11 \right\rangle}^{-1} + 110 {\left\langle x - 12 \right\rangle}^{-1}\]
V = -sym.integrate(qz.expand(), x) + CV
M = sym.integrate(V, x) + CM
kappa = M / EI
phi = sym.integrate(kappa, x) + Cphi
uz = -sym.integrate(phi, x) + Cuz
N = -sym.integrate(qx.expand(), x) + CN
epsilon = N / EA
ux = sym.integrate(epsilon, x) + Cux
uvz = uz.subs(x,0) * sym.cos(o0)
uvx = -ux.subs(x,0) * sym.sin(o0)
for i in range(len(oo)):
uvz += ((uz - uz.subs(x,aa[i])) * sym.SingularityFunction(x,aa[i],0) - (uz - uz.subs(x,aa[i+1])) * sym.SingularityFunction(x,aa[i+1],0)) * sym.cos(oo[i])
uvx += -((ux - ux.subs(x,aa[i])) * sym.SingularityFunction(x,aa[i],0) - (ux - ux.subs(x,aa[i+1])) * sym.SingularityFunction(x,aa[i+1],0)) * sym.sin(oo[i])
uv = uvz + uvx
uhz = uz.subs(x,0) * sym.sin(o0)
uhx = ux.subs(x,0) * sym.cos(o0)
for i in range(len(oo)):
uhz += ((uz - uz.subs(x,aa[i])) * sym.SingularityFunction(x,aa[i],0) - (uz - uz.subs(x,aa[i+1])) * sym.SingularityFunction(x,aa[i+1],0)) * sym.sin(oo[i])
uhx += ((ux - ux.subs(x,aa[i])) * sym.SingularityFunction(x,aa[i],0) - (ux - ux.subs(x,aa[i+1])) * sym.SingularityFunction(x,aa[i+1],0)) * sym.cos(oo[i])
uh = uhz + uhx
display(sym.symbols('{N}='), N)
display(sym.symbols('{V}='), V)
display(sym.symbols('{M}='), M)
display(sym.symbols('{u_x}='), ux)
display(sym.symbols('{\phi}='), phi)
display(sym.symbols('{u_z}='), uz)
display(sym.symbols('{u_v}='), uv)
display(sym.symbols('{u_h}='), uh)
\[\displaystyle {N}=\]
\[\displaystyle C_{N} - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{-1} - H^{BE} {\left\langle x - 2 \right\rangle}^{0} + H^{BE} {\left\langle x - 6 \right\rangle}^{0} + H^{BE} {\left\langle x - 7 \right\rangle}^{0} - H^{BE} {\left\langle x - 11 \right\rangle}^{0} + H^{CD} {\left\langle x - 7 \right\rangle}^{0} - H^{CD} {\left\langle x - 11 \right\rangle}^{0} - H^{CD} {\left\langle x - 12 \right\rangle}^{0} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{0} - R^{A}_{h} {\left\langle x \right\rangle}^{0} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{0} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{0} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{0} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{0} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{0} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{0} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{0} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{0} - V^{BE} {\left\langle x - 6 \right\rangle}^{0} + V^{BE} {\left\langle x - 7 \right\rangle}^{0} + V^{BE} {\left\langle x - 11 \right\rangle}^{0} - V^{BE} {\left\langle x - 12 \right\rangle}^{0} - V^{CD} {\left\langle x - 6 \right\rangle}^{0} + V^{CD} {\left\langle x - 7 \right\rangle}^{0} + V^{CD} {\left\langle x - 11 \right\rangle}^{0} - V^{CD} {\left\langle x - 12 \right\rangle}^{0} - 110 {\left\langle x - 6 \right\rangle}^{0} + 110 {\left\langle x - 7 \right\rangle}^{0} + 110 {\left\langle x - 11 \right\rangle}^{0} - 110 {\left\langle x - 12 \right\rangle}^{0}\]
\[\displaystyle {V}=\]
\[\displaystyle C_{V} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{-2} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{-3} + H^{BE} {\left\langle x - 6 \right\rangle}^{0} - H^{BE} {\left\langle x - 7 \right\rangle}^{0} - H^{BE} {\left\langle x - 11 \right\rangle}^{0} + H^{BE} {\left\langle x - 12 \right\rangle}^{0} + H^{CD} {\left\langle x - 6 \right\rangle}^{0} - H^{CD} {\left\langle x - 7 \right\rangle}^{0} - H^{CD} {\left\langle x - 11 \right\rangle}^{0} + H^{CD} {\left\langle x - 12 \right\rangle}^{0} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{0} - R^{A}_{h} {\left\langle x - 7 \right\rangle}^{0} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{0} + R^{A}_{h} {\left\langle x - 12 \right\rangle}^{0} - R^{A}_{v} {\left\langle x \right\rangle}^{0} + R^{A}_{v} {\left\langle x - 6 \right\rangle}^{0} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{0} - R^{A}_{v} {\left\langle x - 11 \right\rangle}^{0} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{0} - R^{F}_{v} {\left\langle x - 14 \right\rangle}^{0} - T^{BE} {\left\langle x - 2 \right\rangle}^{-1} + T^{BE} {\left\langle x - 12 \right\rangle}^{-1} - T^{CD} {\left\langle x - 6 \right\rangle}^{-1} + T^{CD} {\left\langle x - 12.0 \right\rangle}^{-1} - V^{BE} {\left\langle x - 2 \right\rangle}^{0} + V^{BE} {\left\langle x - 6 \right\rangle}^{0} + V^{BE} {\left\langle x - 7 \right\rangle}^{0} - V^{BE} {\left\langle x - 11 \right\rangle}^{0} + V^{CD} {\left\langle x - 7 \right\rangle}^{0} - V^{CD} {\left\langle x - 11 \right\rangle}^{0} - V^{CD} {\left\langle x - 12 \right\rangle}^{0} + V^{CD} {\left\langle x - 12.0 \right\rangle}^{0} - 10 {\left\langle x \right\rangle}^{1} - 50 {\left\langle x - 4 \right\rangle}^{0} + 110 {\left\langle x - 6 \right\rangle}^{0} + 10 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{0} - 110 {\left\langle x - 11 \right\rangle}^{0} - 110 {\left\langle x - 12 \right\rangle}^{0} - 10 {\left\langle x - 12.0 \right\rangle}^{1}\]
\[\displaystyle {M}=\]
\[\displaystyle C_{M} + C_{V} x - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{-1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{-2} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} - H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{BE} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 6 \right\rangle}^{1} - H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 12 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - R^{F}_{v} {\left\langle x - 14 \right\rangle}^{1} - T^{BE} {\left\langle x - 2 \right\rangle}^{0} + T^{BE} {\left\langle x - 12 \right\rangle}^{0} - T^{CD} {\left\langle x - 6 \right\rangle}^{0} + T^{CD} {\left\langle x - 12.0 \right\rangle}^{0} - V^{BE} {\left\langle x - 2 \right\rangle}^{1} + V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} - V^{BE} {\left\langle x - 11 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} - V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} + V^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - 5 {\left\langle x \right\rangle}^{2} - 50 {\left\langle x - 4 \right\rangle}^{1} + 110 {\left\langle x - 6 \right\rangle}^{1} + 5 {\left\langle x - 6 \right\rangle}^{2} + 110 {\left\langle x - 7 \right\rangle}^{1} - 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1} - 5 {\left\langle x - 12.0 \right\rangle}^{2}\]
\[\displaystyle {u_x}=\]
\[\displaystyle C_{ux} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\]
\[\displaystyle {\phi}=\]
\[\displaystyle C_{\phi} + \frac{C_{M} x + \frac{C_{V} x^{2}}{2} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{0} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{-1} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{2}}{2} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{2}}{2} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{2}}{2} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{2}}{2} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{2}}{2} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{2}}{2} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{2}}{2} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{2}}{2} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{2}}{2} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{2}}{2} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{2}}{2} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{2}}{2} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{2}}{2} - T^{BE} {\left\langle x - 2 \right\rangle}^{1} + T^{BE} {\left\langle x - 12 \right\rangle}^{1} - T^{CD} {\left\langle x - 6 \right\rangle}^{1} + T^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{2}}{2} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{2}}{2} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{2}}{2} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{2}}{2} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{5 {\left\langle x \right\rangle}^{3}}{3} - 25 {\left\langle x - 4 \right\rangle}^{2} + 55 {\left\langle x - 6 \right\rangle}^{2} + \frac{5 {\left\langle x - 6 \right\rangle}^{3}}{3} + 55 {\left\langle x - 7 \right\rangle}^{2} - 55 {\left\langle x - 11 \right\rangle}^{2} - 55 {\left\langle x - 12 \right\rangle}^{2} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{3}}{3}}{EI}\]
\[\displaystyle {u_z}=\]
\[\displaystyle - C_{\phi} x + C_{uz} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\]
\[\displaystyle {u_v}=\]
\[\displaystyle C_{uz} + \left(- C_{\phi} x - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x \right\rangle}^{0} + \left(- \frac{6 C_{N} - 4 H^{BE} - 6 R^{A}_{h}}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 6 \right\rangle}^{0} + \left(- \frac{12 C_{N} + 4 H^{CD} - 2 R^{A}_{h}}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 12 \right\rangle}^{0} - \left(- \frac{7 C_{N} - 4 H^{BE} - 6 R^{A}_{h} - R^{A}_{v} - V^{BE} - V^{CD} - 110}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 7 \right\rangle}^{0} - \left(- \frac{11 C_{N} + 4 H^{CD} - 2 R^{A}_{h} - R^{A}_{v} - V^{BE} - V^{CD} - 110}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 11 \right\rangle}^{0} - \left(- C_{\phi} x + 6 C_{\phi} + \frac{18 C_{M} + 36 C_{V} - 36 R^{A}_{v} - 8 T^{BE} - \frac{32 V^{BE}}{3} - \frac{1820}{3}}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 6 \right\rangle}^{0} - \left(- C_{\phi} x + 7 C_{\phi} + \frac{\frac{49 C_{M}}{2} + \frac{343 C_{V}}{6} + \frac{H^{BE}}{6} + \frac{H^{CD}}{6} + \frac{R^{A}_{h}}{6} - 57 R^{A}_{v} - \frac{25 T^{BE}}{2} - \frac{T^{CD}}{2} - \frac{62 V^{BE}}{3} - \frac{3620}{3}}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 7 \right\rangle}^{0} + \left(- C_{\phi} x + 11 C_{\phi} + \frac{\frac{121 C_{M}}{2} + \frac{1331 C_{V}}{6} + \frac{61 H^{BE}}{6} + \frac{61 H^{CD}}{6} + \frac{61 R^{A}_{h}}{6} - \frac{571 R^{A}_{v}}{3} - \frac{81 T^{BE}}{2} - \frac{25 T^{CD}}{2} - 90 V^{BE} + \frac{32 V^{CD}}{3} - \frac{15700}{3}}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 11 \right\rangle}^{0} + \left(- C_{\phi} x + 12 C_{\phi} + \frac{72 C_{M} + 288 C_{V} + 15 H^{BE} + 15 H^{CD} + 15 R^{A}_{h} - \frac{694 R^{A}_{v}}{3} - 50 T^{BE} - 18 T^{CD} - 110 V^{BE} + \frac{62 V^{CD}}{3} - \frac{18400}{3}}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 12 \right\rangle}^{0} - \left(- C_{\phi} x + 14 C_{\phi} + \frac{98 C_{M} + \frac{1372 C_{V}}{3} - 3.99999999999999 EI \phi^{BC} - EI u^{BC}_{z} + 25 H^{BE} + 25 H^{CD} + 25 R^{A}_{h} - \frac{962 R^{A}_{v}}{3} - 70 T^{BE} - 30.0 T^{CD} - 150 V^{BE} + 52.6666666666667 V^{CD} - 7606.66666666667}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 14 \right\rangle}^{0}\]
\[\displaystyle {u_h}=\]
\[\displaystyle C_{ux} - \left(- \frac{6 C_{N} - 4 H^{BE} - 6 R^{A}_{h}}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 6 \right\rangle}^{0} + \left(- \frac{12 C_{N} + 4 H^{CD} - 2 R^{A}_{h}}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 12 \right\rangle}^{0} - \left(- \frac{14 C_{N} - EA u^{BC}_{x} + 4.0 H^{CD} - 4 R^{A}_{h}}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 14 \right\rangle}^{0} - \left(- \frac{7 C_{N} - 4 H^{BE} - 6 R^{A}_{h} - R^{A}_{v} - V^{BE} - V^{CD} - 110}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 7 \right\rangle}^{0} + \left(- \frac{11 C_{N} + 4 H^{CD} - 2 R^{A}_{h} - R^{A}_{v} - V^{BE} - V^{CD} - 110}{EA} + \frac{C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}}{EA}\right) {\left\langle x - 11 \right\rangle}^{0} - \left(- C_{\phi} x + 6 C_{\phi} + \frac{18 C_{M} + 36 C_{V} - 36 R^{A}_{v} - 8 T^{BE} - \frac{32 V^{BE}}{3} - \frac{1820}{3}}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 6 \right\rangle}^{0} + \left(- C_{\phi} x + 7 C_{\phi} + \frac{\frac{49 C_{M}}{2} + \frac{343 C_{V}}{6} + \frac{H^{BE}}{6} + \frac{H^{CD}}{6} + \frac{R^{A}_{h}}{6} - 57 R^{A}_{v} - \frac{25 T^{BE}}{2} - \frac{T^{CD}}{2} - \frac{62 V^{BE}}{3} - \frac{3620}{3}}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 7 \right\rangle}^{0} + \left(- C_{\phi} x + 11 C_{\phi} + \frac{\frac{121 C_{M}}{2} + \frac{1331 C_{V}}{6} + \frac{61 H^{BE}}{6} + \frac{61 H^{CD}}{6} + \frac{61 R^{A}_{h}}{6} - \frac{571 R^{A}_{v}}{3} - \frac{81 T^{BE}}{2} - \frac{25 T^{CD}}{2} - 90 V^{BE} + \frac{32 V^{CD}}{3} - \frac{15700}{3}}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 11 \right\rangle}^{0} - \left(- C_{\phi} x + 12 C_{\phi} + \frac{72 C_{M} + 288 C_{V} + 15 H^{BE} + 15 H^{CD} + 15 R^{A}_{h} - \frac{694 R^{A}_{v}}{3} - 50 T^{BE} - 18 T^{CD} - 110 V^{BE} + \frac{62 V^{CD}}{3} - \frac{18400}{3}}{EI} - \frac{\frac{C_{M} x^{2}}{2} + \frac{C_{V} x^{3}}{6} - 2 EI \phi^{BC} {\left\langle x - 12.0 \right\rangle}^{1} - EI u^{BC}_{z} {\left\langle x - 12.0 \right\rangle}^{0} + \frac{H^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{BE} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{H^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{H^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 6 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{h} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{R^{A}_{h} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{R^{A}_{v} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{R^{A}_{v} {\left\langle x - 12 \right\rangle}^{3}}{6} - \frac{R^{F}_{v} {\left\langle x - 14 \right\rangle}^{3}}{6} - \frac{T^{BE} {\left\langle x - 2 \right\rangle}^{2}}{2} + \frac{T^{BE} {\left\langle x - 12 \right\rangle}^{2}}{2} - \frac{T^{CD} {\left\langle x - 6 \right\rangle}^{2}}{2} + \frac{T^{CD} {\left\langle x - 12.0 \right\rangle}^{2}}{2} - \frac{V^{BE} {\left\langle x - 2 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 6 \right\rangle}^{3}}{6} + \frac{V^{BE} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{BE} {\left\langle x - 11 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 7 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 11 \right\rangle}^{3}}{6} - \frac{V^{CD} {\left\langle x - 12 \right\rangle}^{3}}{6} + \frac{V^{CD} {\left\langle x - 12.0 \right\rangle}^{3}}{6} - \frac{5 {\left\langle x \right\rangle}^{4}}{12} - \frac{25 {\left\langle x - 4 \right\rangle}^{3}}{3} + \frac{55 {\left\langle x - 6 \right\rangle}^{3}}{3} + \frac{5 {\left\langle x - 6 \right\rangle}^{4}}{12} + \frac{55 {\left\langle x - 7 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 11 \right\rangle}^{3}}{3} - \frac{55 {\left\langle x - 12 \right\rangle}^{3}}{3} - \frac{5 {\left\langle x - 12.0 \right\rangle}^{4}}{12}}{EI}\right) {\left\langle x - 12 \right\rangle}^{0} + \frac{\left(C_{N} x - EA u^{BC}_{x} {\left\langle x - 12.0 \right\rangle}^{0} - H^{BE} {\left\langle x - 2 \right\rangle}^{1} + H^{BE} {\left\langle x - 6 \right\rangle}^{1} + H^{BE} {\left\langle x - 7 \right\rangle}^{1} - H^{BE} {\left\langle x - 11 \right\rangle}^{1} + H^{CD} {\left\langle x - 7 \right\rangle}^{1} - H^{CD} {\left\langle x - 11 \right\rangle}^{1} - H^{CD} {\left\langle x - 12 \right\rangle}^{1} + H^{CD} {\left\langle x - 12.0 \right\rangle}^{1} - R^{A}_{h} {\left\langle x \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{h} {\left\langle x - 7 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{h} {\left\langle x - 12 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 6 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 7 \right\rangle}^{1} + R^{A}_{v} {\left\langle x - 11 \right\rangle}^{1} - R^{A}_{v} {\left\langle x - 12 \right\rangle}^{1} - V^{BE} {\left\langle x - 6 \right\rangle}^{1} + V^{BE} {\left\langle x - 7 \right\rangle}^{1} + V^{BE} {\left\langle x - 11 \right\rangle}^{1} - V^{BE} {\left\langle x - 12 \right\rangle}^{1} - V^{CD} {\left\langle x - 6 \right\rangle}^{1} + V^{CD} {\left\langle x - 7 \right\rangle}^{1} + V^{CD} {\left\langle x - 11 \right\rangle}^{1} - V^{CD} {\left\langle x - 12 \right\rangle}^{1} - 110 {\left\langle x - 6 \right\rangle}^{1} + 110 {\left\langle x - 7 \right\rangle}^{1} + 110 {\left\langle x - 11 \right\rangle}^{1} - 110 {\left\langle x - 12 \right\rangle}^{1}\right) {\left\langle x \right\rangle}^{0}}{EA}\]
# 3 reactiekrachten + 6 knoopkrachten + 3 vervormingssprongen + 6 integratieconstanten = 18 voorwaarden
Eq1 = sym.Eq(N.subs(x,a0-dx),0)
Eq2 = sym.Eq(N.subs(x,a5+dx),0)
Eq3 = sym.Eq(N.subs(x,a6+dx),0)
Eq4 = sym.Eq(V.subs(x,0-dx),0)
Eq5 = sym.Eq(V.subs(x,a5+dx),0)
Eq6 = sym.Eq(V.subs(x,a6+dx),0)
Eq7 = sym.Eq(M.subs(x,a0-dx),0)
Eq8 = sym.Eq(M.subs(x,a5+dx),0)
Eq9 = sym.Eq(M.subs(x,a6+dx),0)
Eq10 = sym.Eq(phi.subs(x,a5+dx)-phi.subs(x,a1),0)
Eq11 = sym.Eq(phi.subs(x,s1+dx)-phi.subs(x,a2),0)
Eq12 = sym.Eq(uv.subs(x,0),0)
Eq13 = sym.Eq(uv.subs(x,a5)-uv.subs(x,a1),0)
Eq14 = sym.Eq(uv.subs(x,s1)-uv.subs(x,a2),0)
Eq15 = sym.Eq(uv.subs(x,a6),0)
Eq16 = sym.Eq(uh.subs(x,0),0)
Eq17 = sym.Eq(uh.subs(x,a5)-uh.subs(x,a1),0)
Eq18 = sym.Eq(uh.subs(x,s1)-uh.subs(x,a2),0)
sol = sym.solve((Eq1,Eq2,Eq3,Eq4,Eq5,Eq6,Eq7,Eq8,Eq9,Eq10,Eq11,Eq12,Eq13,Eq14,Eq15,Eq16,Eq17,Eq18),(RvA,RhA,RvF,VBE,HBE,TBE,VCD,HCD,TCD,phiBC,uzBC,uxBC,CN,CV,CM,Cphi,Cuz,Cux))
display(sol)
{C_M: 0.0,
C_N: 0.0,
C_V: 0.0,
C_phi: (-4.40975360000001e+45*EA**2 - 3.08877312e+46*EA*EI - 3.2587776e+45*EI**2)/(2.79552e+43*EA**2*EI + 1.062144e+44*EA*EI**2 + 1.10592e+43*EI**3),
C_ux: 0.0,
C_uz: 0.0,
H^BE: 5.696e+31*EA/(4.16e+29*EA + 1.536e+30*EI),
H^CD: 0.0,
R_h^A: 0.0,
R_v^A: -65.0000000000000,
R_v^F: -65.0000000000000,
T^BE: (4.465664e+33*EA**2 + 8.133888e+33*EA*EI + 8.20223999999999e+32*EI**2)/(3.4944e+31*EA**2 + 1.32768e+32*EA*EI + 1.3824e+31*EI**2),
T^CD: 110.000000000000,
V^BE: -3.69482222595252e+15*EA/(8.96e+29*EA + 9.6e+28*EI),
V^CD: -45.0000000000000,
phi^BC: (-1.7088e+31*EA - 2.73408e+32*EI)/(4.16e+29*EA*EI + 1.536e+30*EI**2),
u_x^BC: (2.848e+58*EA + 1.09139364212751e+43*EI)/(5.2e+55*EA**2 + 1.92e+56*EA*EI),
u_z^BC: (-9.14720432611493e+29*EA - 9.82168933355715e+28*EI)/(1.792e+41*EA*EI + 1.92e+40*EI**2)}
#display(sym.simplify(uz.subs(sol).rewrite(sym.Piecewise)))
ea = 10**3
ei = 3*10**3
display(f'{RvA} = {RvA.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{RhA} = {RhA.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{RvF} = {RvF.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{VBE} = {VBE.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{HBE} = {HBE.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{TBE} = {TBE.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{VCD} = {VCD.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{HCD} = {HCD.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{TCD} = {TCD.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{phiBC} = {phiBC.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')
display(f'{uzBC} = {uzBC.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')
display(f'{uxBC} = {uxBC.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')
display(f'{CN} = {CN.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{CV} = {CV.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{CM} = {CM.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{Cphi} = {Cphi.subs(sol).subs(EI,ei).subs(EA,ea):.4f}')
display(f'{Cux} = {Cux.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
display(f'{Cuz} = {Cuz.subs(sol).subs(EI,ei).subs(EA,ea):.2f}')
'R_v^A = -65.00'
'R_h^A = 0.00'
'R_v^F = -65.00'
'V^BE = -0.00'
'H^BE = 11.34'
'T^BE = 65.00'
'V^CD = -45.00'
'H^CD = 0.00'
'T^CD = 110.00'
'phi^BC = -0.0556'
'u_z^BC = -0.0000'
'u_x^BC = 0.0454'
'C_N = 0.00'
'C_V = 0.00'
'C_M = 0.00'
'C_phi = -0.0944'
'C_ux = 0.00'
'C_uz = 0.00'
vBE, hBE = sym.symbols('v^BE h^BE')
vv = [vBE]
hh = [hBE]
v = 0
h = 0
for i in range(len(oo)):
v += -(sym.SingularityFunction(x,aa[i],1) - sym.SingularityFunction(x,aa[i+1],1)) * sym.sin(oo[i])
h += (sym.SingularityFunction(x,aa[i],1) - sym.SingularityFunction(x,aa[i+1],1)) * sym.cos(oo[i])
for i in range(len(ss)):
v += vv[i] * sym.SingularityFunction(x,ss[i],0)
h += hh[i] * sym.SingularityFunction(x,ss[i],0)
# 1 x 2 sprongen = 2 onbekenden
Eq1 = sym.Eq(v.subs(x,a2),v.subs(x,s1))
Eq2 = sym.Eq(h.subs(x,a2),h.subs(x,s1))
sol2 = sym.solve((Eq1,Eq2),(vBE, hBE))
display(sol2)
{h^BE: 4.00000000000000, v^BE: 0.0}
L = aa[-1]
x_np = np.linspace(0-dx,L+dx,10000)
ab = aa
ab.extend(bb)
ab.sort()
ab = list(dict.fromkeys(ab))
N_np = sym.lambdify(x, N.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))
display(N.subs(sol).subs(EI,ei).subs(EA,ea))
for i in range(len(ab)):
display(f'N({ab[i]}) = {N.subs(x,ab[i]).subs(sol).subs(EI,ei).subs(EA,ea)} [kN]')
plt.figure(figsize=(10,4))
plt.plot(x_np,N_np(x_np))
plt.xlabel('$x$')
plt.ylabel('$N$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
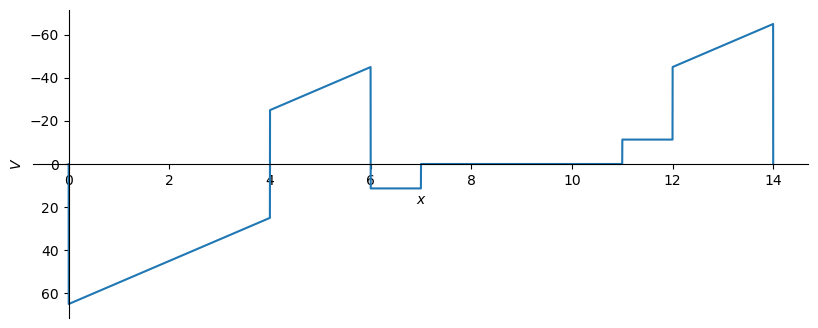
\[\displaystyle - 11.3375796178344 {\left\langle x - 2 \right\rangle}^{0} + 11.3375796178344 {\left\langle x - 6 \right\rangle}^{0} + 11.3375796178344 {\left\langle x - 7 \right\rangle}^{0} - 11.3375796178344 {\left\langle x - 11 \right\rangle}^{0} + 3.12062688002747 \cdot 10^{-15} {\left\langle x - 12 \right\rangle}^{0} - 45.3503184713376 {\left\langle x - 12.0 \right\rangle}^{-1}\]
'N(0) = 0 [kN]'
'N(2) = -11.3375796178344 [kN]'
'N(4) = -11.3375796178344 [kN]'
'N(6) = 3.12062688002747E-15 [kN]'
'N(7) = 11.3375796178344 [kN]'
'N(11) = -3.12062688002747E-15 [kN]'
'N(12) = 0 [kN]'
'N(12.000000000000004) = -oo [kN]'
'N(14) = 0 [kN]'
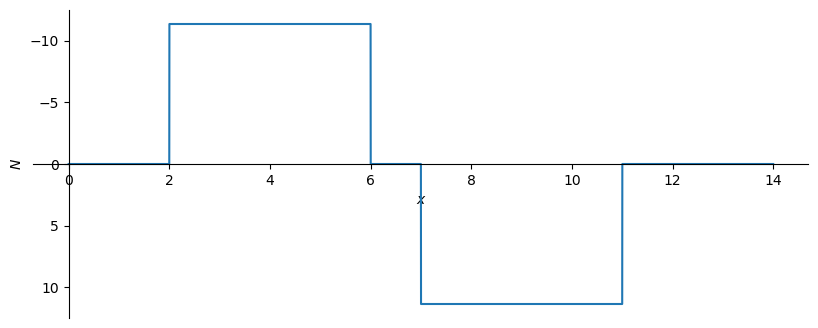
V_np = sym.lambdify(x, V.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))
display(V.subs(sol).subs(EI,ei).subs(EA,ea))
for i in range(len(ab)):
display(f'V({ab[i]}) = {V.subs(x,ab[i]+dx).subs(sol).subs(EI,ei).subs(EA,ea)} [kN]')
plt.figure(figsize=(10,4))
plt.plot(x_np,V_np(x_np))
plt.xlabel('$x$')
plt.ylabel('$V$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
\[\displaystyle 65.0 {\left\langle x \right\rangle}^{0} - 10 {\left\langle x \right\rangle}^{1} - 65.0021231422505 {\left\langle x - 2 \right\rangle}^{-1} + 3.12062688002747 \cdot 10^{-15} {\left\langle x - 2 \right\rangle}^{0} - 50 {\left\langle x - 4 \right\rangle}^{0} - 110.0 {\left\langle x - 6 \right\rangle}^{-1} + 56.3375796178344 {\left\langle x - 6 \right\rangle}^{0} + 10 {\left\langle x - 6 \right\rangle}^{1} - 11.3375796178344 {\left\langle x - 7 \right\rangle}^{0} - 11.3375796178344 {\left\langle x - 11 \right\rangle}^{0} + 65.0021231422505 {\left\langle x - 12 \right\rangle}^{-1} + 11.3375796178344 {\left\langle x - 12 \right\rangle}^{0} + 5.10714152288094 \cdot 10^{-12} {\left\langle x - 12.0 \right\rangle}^{-3} + 333.324840764331 {\left\langle x - 12.0 \right\rangle}^{-2} + 110.0 {\left\langle x - 12.0 \right\rangle}^{-1} - 45.0 {\left\langle x - 12.0 \right\rangle}^{0} - 10 {\left\langle x - 12.0 \right\rangle}^{1} + 65.0 {\left\langle x - 14 \right\rangle}^{0}\]
'V(0) = 65.0000000000000 [kN]'
'V(2) = 45.0000000000000 [kN]'
'V(4) = -25.0000000000000 [kN]'
'V(6) = 11.3375796178344 [kN]'
'V(7) = -3.12062688002747E-15 [kN]'
'V(11) = -11.3375796178344 [kN]'
'V(12) = 0 [kN]'
'V(12.000000000000004) = -45.0000000000000 [kN]'
'V(14) = 0 [kN]'
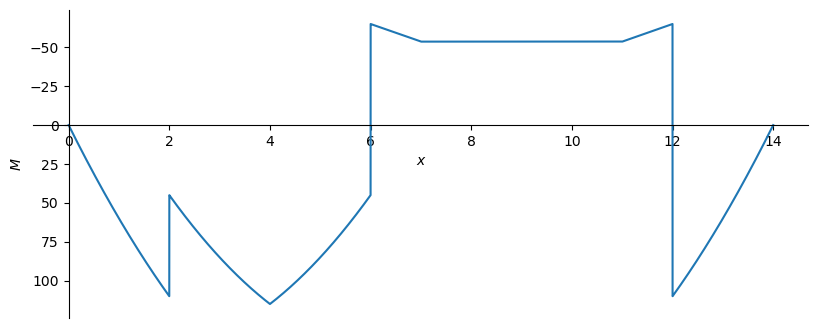
M_np = sym.lambdify(x, M.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))
for i in range(len(ab)):
display(f'M({ab[i]}) = {M.subs(x,ab[i]).subs(sol).subs(EI,ei).subs(EA,ea)} [kNm]')
plt.figure(figsize=(10,4))
plt.plot(x_np,M_np(x_np))
plt.xlabel('$x$')
plt.ylabel('$M$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
'M(0) = 0.0 [kNm]'
'M(2) = 44.9978768577495 [kNm]'
'M(4) = 114.997876857749 [kNm]'
'M(6) = -65.0021231422505 [kNm]'
'M(7) = -53.6645435244161 [kNm]'
'M(11) = -53.6645435244161 [kNm]'
'M(12) = 2.84217094304040E-14 [kNm]'
'M(12.000000000000004) = oo [kNm]'
'M(14) = 5.68434188608080E-14 [kNm]'
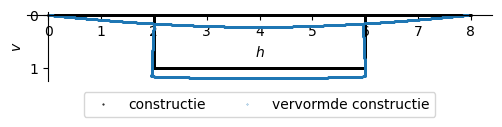
v_np = sym.lambdify(x, v.subs(sol2).rewrite(sym.Piecewise))
h_np = sym.lambdify(x, h.subs(sol2).rewrite(sym.Piecewise))
uv_np = sym.lambdify(x, uv.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))
uh_np = sym.lambdify(x, uh.subs(sol).subs(EI,ei).subs(EA,ea).rewrite(sym.Piecewise))
#display(uv.subs(sol))
for i in range(len(ab)):
display(f'uv({ab[i]:.1f}) = {uv.subs(x,ab[i]).subs(sol).subs(EI,ei).subs(EA,ea):.4f} [m]')
for i in range(len(ab)):
display(f'uh({ab[i]:.1f}) = {uh.subs(x,ab[i]).subs(sol).subs(EI,ei).subs(EA,ea):.4f} [m]')
plt.figure(figsize=(6,6))
plt.plot(h_np(x_np),v_np(x_np), marker='.',markersize=1, linewidth=0, color='black', label='constructie')
plt.plot((h_np(x_np)+uh_np(x_np)),(v_np(x_np)+uv_np(x_np)), marker='.',markersize=0.5, linewidth=0, label='vervormde constructie')
plt.xlabel('$h$')
plt.ylabel('$v$');
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['left'].set_position('zero')
ax.invert_yaxis()
plt.axis('scaled')
ax.legend(loc='upper center', bbox_to_anchor=(0.5, -0.05),fancybox=True, shadow=False, ncol=3);
'uv(0.0) = 0.0000 [m]'
'uv(2.0) = 0.1622 [m]'
'uv(4.0) = 0.2256 [m]'
'uv(6.0) = 0.1622 [m]'
'uv(7.0) = 0.1622 [m]'
'uv(11.0) = 0.1622 [m]'
'uv(12.0) = 0.1622 [m]'
'uv(12.0) = 0.1622 [m]'
'uv(14.0) = 0.0000 [m]'
'uh(0.0) = 0.0000 [m]'
'uh(2.0) = 0.0000 [m]'
'uh(4.0) = -0.0227 [m]'
'uh(6.0) = -0.0454 [m]'
'uh(7.0) = -0.0000 [m]'
'uh(11.0) = -0.0454 [m]'
'uh(12.0) = -0.0000 [m]'
'uh(12.0) = -0.0454 [m]'
'uh(14.0) = -0.0454 [m]'