16.2. Global dimensioning column#
Note
The calculations serve as examples for educational purposes and not as guidance for practice.
Estimation rules also exist for columns, but especially for these elements, the actual dimensions required can be very different from those found with these estimation rules. The dimensions of the column depend strongly on the buckling length. However, there is a big difference whether a column has to support an entire building with many floors or just the roof. Often, the column at ground level is the ‘dimensional’ column. A slender column with large buckling length could also be normative, even if it is not on the ground floor.
Note that for the b and for the I, the weakest direction should always apply: For HEA profiles, we therefore do not take the profile height but the width of the profile and \(I_z\). Precisely this direction is the weakest and (usually) determines buckling out.
We are going to dimension and check column D3 under the 1st floor for the office. To perform the check, we need to know what load the column has to bear. To do this, we first create a load diagram and then a weight calculation that we tabulate.
The load diagram consists of all schematic DC plans (or a 3D drawing) showing the column in question and all structural members resting on it: Columns and beams possibly by colour and the floor area by shading. All beams within the shaded areas transfer their load to the column. We also show the length dimensions so that the total load to be carried by the column can be easily determined. The load diagram also includes collecting the loads on the column.
Note
For the concrete structure, this was a beam of 300 mm by 600 mm, made of concrete with a strength class C35/45 and a weight of \(4.5 [kN/m]\).
For simplicity, we assume that the permanent load of the roof is equal to that of the floors. The roof beams are the same as those in the floor. Depending on the roof covering, the difference will not be significant. According to the Eurocode, for a roof not used as a terrace, an imposed load of \(1 [kN/m^2]\) should be taken for every \(10 [m^2]\) of roof area. For the entire roof, a lower imposed load can be considered. However, we choose an imposed load of \(1 [kN/m^2]\). This also provides the option for installing solar panels (PV panels) or adding a light sedum planting. It is advisable to consistently record the data found for clarity. The table below summarises the loads.
Opgelegde belasting |
Opgelegde belasting |
Rustende belasting |
Rustende belasting |
Gewicht ligger |
Gewicht ligger |
|
|---|---|---|---|---|---|---|
vloer |
dak |
vloer |
dak |
vloer |
dak |
|
[kN/m^2] |
[kN/m^2] |
[kN/m^2] |
[kN/m^2] |
[kN/m] |
[kN/m] |
|
betonskelet |
3 |
1 |
4.9 |
4.9 |
4.5 |
4.5 |
Note
For a concrete column, we need to gather some data. The most common choice is a square column. Using the estimation rule, we obtain a column: \(3600 / 10 = 360 [mm]\). The weight of the column is thus
\(0.36 [m] × 0.36 [m] × 25 [kN/m^3] = 3.24 [kN/m]\).
We can calculate the values for A and I using the mechanics formulas for cross-sections.
\(b_{kolom}\) [mm] |
Profile [mm^2] |
Weight [N/mm] |
A [mm^2] |
\(\mathsf{I_z}\) [mm^4] |
Strength class |
Strength [N/mm^2] |
Modulus of Elasticity [N/mm^2] |
|---|---|---|---|---|---|---|---|
360 |
360x360 |
3.24 |
129600 |
\(1399.7 \cdot 10^6\) |
C30/37 |
20 |
\(27.5 \cdot 10^3\) |
For the modulus of elasticity, we must use the design value \(\mathsf{E_{c,d}}\) according to the standard.
Weight table#
The load is schematically represented as a point load on the column. All loads must therefore be converted to a load in kN. This can be done systematically with a weight table. This table calculates all loads on the column, per floor. The following pages show a weight table for the steel and the concrete column.
The weight of columns and beams (given in kN per m) must be multiplied by the respective floor height and beam length to obtain a point load: [kN/m] \(\Rightarrow\) [kN].
The imposed load and the permanent floor load are determined in [kN/m^2]. Therefore, they must be multiplied by the area in [m^2] that is supported by the respective column: [kN/m^2] \(\Rightarrow\) [kN]. To facilitate calculation, we’ll place the table in an Excel spreadsheet as shown in the figures below.
According to the standard committee, the probability of all floors being extremely loaded is almost nil. Therefore, for the variable load, the combination factor \(\psi_0\) (formerly called the moment factor) has been introduced. This is a reduction factor that should be used for almost all floors except two.
For the two floors that contribute the most to the variable load, this should be taken extremely (\(\psi_0=1\)).
For the other floors, \(\psi_0\) depends on the use of the floor. For offices, according to the National Annex to the Eurocode, \(\psi_0 = 0.5\). For the roof, \(\psi_0 = 0\) can even be taken (but not if we consider the column under the roof or under the top floor). The formula for the total load on the column is:
\(\gamma_{G}\) and \(\gamma_{Q}\) are the (partial) safety factors.

Control calculation column (compressive strength)#
From the column, we will verify the compressive strength and determine the slenderness ratio \(n\).
For the compressive stress, we have:
Where:
\(A\) is the cross-sectional area.
\(f_{c;d}\) is the compressive strength.
We can also perform the Unity Check here:
If the strength is not satisfied, then we can multiply the found \(A\) by the value of the Unity Check to obtain the required cross-section:
Note
From the weight table, it appears that the concrete column on the ground floor (under the first floor) must support 1854.5 kN. The stress in the column is:
\(\sigma_{c;d}=\dfrac{F_{c;d}}{A}=\dfrac{1854.7 \cdot 10^3 [N]}{360 [mm] \cdot 360 [mm]}=14.3 [N/mm^2]\)
The Unity Check for the \(360 \times 360 [mm^2]\) concrete column is:
\(U.C. \Rightarrow \dfrac{\sigma_{c;d}}{f_{c;d}}=\dfrac{14.3 [N/mm^2]}{20 [N/mm^2]}=0.72 < 1.0\) \(\Rightarrow \textcolor{green}{\text{Meets Requirement}}\)
The chosen dimensions of the column meet the requirement, but the unity check is so low that we can choose a more optimal size to save material. The minimum required dimensions of the column can be determined by calculating the required cross-sectional area:
\(A_{necessary} = U.C. \cdot A_{old} = 0.72 \cdot 360 [mm] \cdot 360 [mm] = 93312 [mm^2]\)
For a square column, the dimensions would be:
\(\sqrt{A} = \sqrt{93312 [mm^2]} = 305 [mm]\)
This dimension is not practical. A column of \(300 \times 300 [mm^2]\) is preferred. This size is possible when using strength class C35/45 with a compressive strength of \(f_c = 23.3 [N/mm^2]\):
\(\sigma_{c;d}=\dfrac{F_{c;d}}{A}=\dfrac{1854.5 \cdot 10^3 [N]}{300 [mm] \cdot 300 [mm]} = 20.6\ [N/mm^2] < 23.3 [N/mm^2]\)
\(U.C. \Rightarrow \dfrac{\sigma_{c;d}}{f_{c;d}}=\dfrac{20.6 [N/mm^2]}{23.3 [N/mm^2]}=0.88 < 1\) \(\Rightarrow \textcolor{green}{\text{Meets Requirement}}\)
Determination of buckling number n#
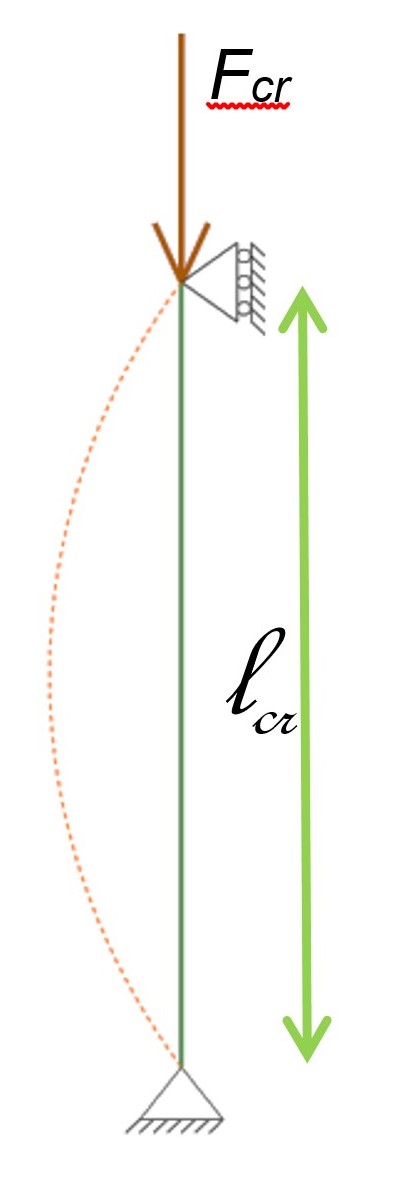
Buckling is a dangerous form of failure that occurs quite suddenly. This problem was recognised long ago. In 1744, the Swiss scholar Leonard Euler came up with the following formula:
\(F_{cr}\) (or \(F_E\)) is called the Euler or critical buckling force.
E represents the modulus of elasticity. For concrete and wood, the modulus of elasticity for UGT should be applied, for concrete \(E_{c,d}\), and for wood \(E_{0,05}\) or, for laminated wood, \(E_{0,gl,05}\).
\(I\) is the quadratic surface moment in the weakest direction!. The weak direction is indicated in the Netherlands with the z in the caption because the weak bending direction is around the z-axis: \(I_z\).
\(l_{cr}\) is the buckling length. In a braced building with hinge connections between columns and beams, the buckling length of the column is equal to the floor height.
Note
For the concrete column of \(\mathsf{360 \cdot 360 [mm^2]}\), we have:
\(F_{cr} = \dfrac{\pi^2 \cdot E \cdot I_z}{l^2_{cr}}=\dfrac{\pi^2 \cdot 27500 [N/mm^2] \cdot 1400 \cdot 10^6 [mm^4]}{(3600 [mm])^2}= 29313 \cdot 10^3 [N]\)
\(n = \dfrac{F_{cr}}{F_{c;d}}= \dfrac{29313 \cdot 10^3 [N]}{1861.1 \cdot 10^3 [N]} = 15.7 \geq 5\)
\(U.C. \Rightarrow \dfrac{5 \cdot F_{c;d}}{F_{cr}}=\dfrac{5 \cdot 1861.1 \cdot 10^3 [N]}{29313 \cdot 10^3 [N]}= 0.32 < 1 \Rightarrow \textcolor{green}{\text{Meets requirement}}\)
The buckling number indicates that the column provides ample safety against buckling. Since the U.C. is so low, we could again consider if material savings are possible. We can determine the minimum required quadratic surface moment of the column using the U.C.:
\(I_{z,required}=U.C.\cdot I_z=0.32 \cdot 1400 \cdot 10^6 [mm^4] = 444 \cdot 10^6 [mm^4]\).
In the stress check, we found a column of \(300 \cdot 300 [mm^2]\). The quadratic surface moment at this cross-section is:
\(I_z=\frac{1}{12} \cdot 300 [mm] \cdot (300 [mm])^3=675 \cdot 10^6 [mm^4]\)
and will therefore also be more than sufficient. Concrete columns often provide sufficient buckling safety due to their relatively large surface area.