18.2. Columns

Note

The calculations serve as examples for educational purposes and not as guidance for practice.

This page provides calculation examples for the structural design of timber columns in accordance with modern engineering principles. It demonstrates key steps for verifying column dimensions, buckling resistance, and material stresses under various load conditions. Through clear examples and detailed calculations, the page illustrates how to optimise timber columns for stability and safety, ensuring compliance with design requirements. Assumptions: column made of laminated timber GL24h, grid 6 m x 6 m, timber floor \(G = 2.0 \, \text{kN/m}^2\), and CC2

\(Q = 2 \, \text{kN/m}^2\), max 3 storeys	\(Q = 2 \, \text{kN/m}^2\), max 5 storeys	\(Q = 5 \, \text{kN/m}^2\), max 3 storeys
\(Q = 2 \, \text{kN/m}^2\)	\(Q = 2 \, \text{kN/m}^2\)	\(Q = 5 \, \text{kN/m}^2\)
\(P_{d} = 5.4 \, \text{kN/m}^2\)	\(P_{d} = 5.4 \, \text{kN/m}^2\)	\(P_{d} = 9.9 \, \text{kN/m}^2\)
\(n = 2 \, \text{storeys}\)	\(n = 4 \, \text{storeys}\)	\(n = 2 \, \text{storeys}\)
\(F_{Gk} = 144 \, \text{kN}\)	\(F_{Gk} = 288 \, \text{kN}\)	\(F_{Gk} = 144 \, \text{kN}\)
\(F_{Qk} = 144 \, \text{kN}\)	\(F_{Qk} = 288 \, \text{kN}\)	\(F_{Qk} = 360 \, \text{kN}\)

import numpy as np
import matplotlib.pyplot as plt

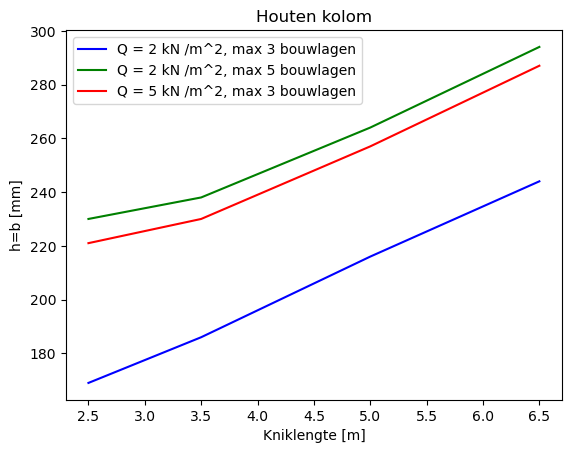
L_buc23 = [2.5, 3.5, 5, 6.5]
hb_23 = [169, 186, 216, 244]

L_buc25 = [2.5, 3.5, 5, 6.5]
hb_25 = [230, 238, 264, 294]

L_buc53 = [2.5, 3.5, 5, 6.5]
hb_53 = [221, 230, 257, 287]

plt.figure()
plt.title('Timber column')
plt.plot(L_buc23, hb_23, c= 'b', label='Q = 2 kN /m^2, max 3 building layers')
plt.plot(L_buc25, hb_25, c= 'g', label='Q = 2 kN /m^2, max 5 building layers')
plt.plot(L_buc53, hb_53, c= 'r', label='Q = 5 kN /m^2, max 3 building layers')
plt.xlabel('Effective length [m]')
plt.ylabel('h=b [mm]')
plt.legend(loc='best');