2.6. Variable loads 3: rain and snow#
Loading by rainwater#
Loads by rainwater are the result of accumulating water due to for example hogging of adjacent roof parts or clogging of the drainage systems. The most practical way of dealing with these actions is converting the snow load to a layer of water (e.g.: \(0,56 kN/m^2\) equals 56 mm water on the roof) and preventing the water from rising above this amount by designing for emergency overflow. Furthermore, always design a roof with a small pitch (general loads, general)

Fig. 2.17 Emergency overflow by means of a so called “mailbox”.#

Fig. 2.18 Emergency overflow by means of locally lowered parapet.#
Snow loads#
Snow can cause considerable loads, as it doesn’t run off like rain. It is therefore important to check whether a load combination containing snow loads is leading. For different parts of Europe the value of the snow load can differ greatly (e.g.: compare the Mediterranean Coast to the Alps). In the Dutch National Annex of NEN-EN 1991-1-3 the complex calculations are substituted by one value for the whole country (\(s_k = 0,7 kN/m^2\)). For other areas NEN-EN 1991-1-3 must be consulted.
Determining the snow loading#
\(s\) = Characteristic value of the snow load on the ground [\(kN/m^2\)] (\(0,7 kN/m^2\) in
the Netherlands)
\(μ_i\) = Shape coefficient, dependend on roof angle α
\(C_e\) = Exposure coefficient (1,0 for most cases)
\(C_t\) = Thermal coefficient (1,0 for most cases)
The shape coefficient can be determined with the shown diagram. Note that μ2 is only applicable where snow accumulation can occur. For complex roof shapes and more information, see NEN-EN 1991-1-3.
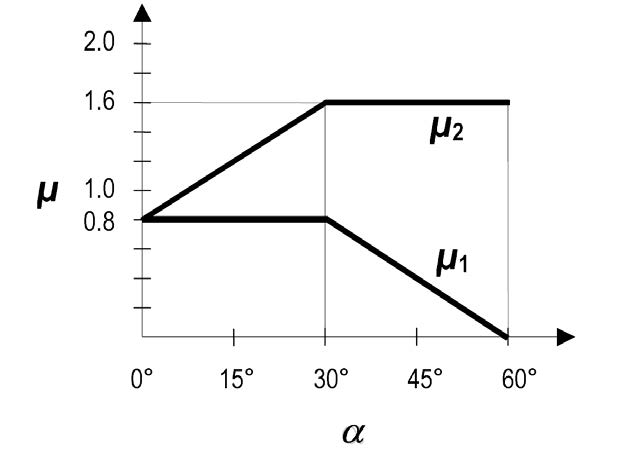
Fig. 2.19 Determining the \(\mu\) factor for snow loading.#