3.2. Cross sectional quantitites

Definition section parameters

Table 3.2 Section parameters.

Surface	Static moment of area	Moment of Inertia	Polar moment of inertia	Steiner’s rule
\(A=\int_A\,dA\)	\(S_y = \int_A y\, dA\)	\(I_{yy}=I_z=\int_A y^2\,dA\)	\(I_p = \int_A r^2\, dA = I_{yy} + I_{zz}\)	\(I_{\overline{yy}}=I_{yy(own)}+\bar{y}_c^2 \cdot A\)
	\(S_z = \int_A z\, dA\)	\(I_{yz}=I_{zy}=\int_A y*z\,dA\)		\(I_{\overline{yz}}=I_{\overline{zy}}=I_{yz(own)}+\bar{y}_c \cdot \bar{z}_c \ A\)
		\(I_{zz}=I_{y}=\int_A z^2\,dA\)		\(I_{\overline{zz}}=I_{zz(own)}+\bar{z}_c^2 \cdot A\)

Section parameters

Square

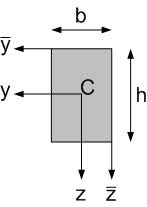
Fig. 3.1 Cross-section of a rectangular shape.

Table 3.3 Section parameters for square cross-sections.

Area, centre of gravity	Moments of intertia own	other
\(A=bh\)	\(I_{yy}=\frac{1}{12}*b^3*h\)	\(I_{\overline{yy}}=1/3b^3h\)
\(\bar{y}_C=\frac{1}{2}b\)	\(I_{zz}=\frac{1}{12}bh^3\)	\(I_{\overline{zz}}=\frac{1}{3}bh^3\)
\(\bar{z}_C=\frac{1}{2}b\)	\(I_{yz}=\frac{1}{12}bh^3\)	\(I_{\overline{yz}}=\frac{1}{4}b^2h^2\)

Parallelogram

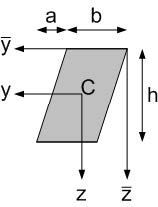
Fig. 3.2 Cross-section of a parallelogram shape.

Table 3.4 Section parameters for parallelogram cross-sections.

Area, centre of gravity	Moments of intertia own	other
\(A=bh\)	\(I_{yy}=\frac{1}{12}(a^2+b^2)\)	\(I_{\overline{yy}}=1/3bh^3\)
\(\bar{y}_C=\frac{1}{2}(a+b)\)	\(I_{zz}=\frac{1}{12}bh^3\)
\(\bar{z_C}=\frac{1}{2}h\)	\(I_{yz}=\frac{1}{12}abh^2\)

Triangle

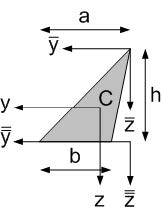
Fig. 3.3 Cross-section of a triangle shape.

Table 3.5 Section parameters for triangle cross-sections.

Area, centre of gravity	Moments of intertia own	other
\(A=\frac{1}{2}bh\)	\(I_{yy}=\frac{1}{36}*(a^2-ab+b^2)\)	\(I_{\overline{zz}}=\frac{1}{3}bh^3\)
\(\bar{y}_C=\frac{1}{3}(2a-b)\)	\(I_{zz}=\frac{1}{36}bh^3\)	\(I_{\overline{yz}}=\frac{1}{8}(2a-b)bh^2\)
\(\bar{z}_C=\frac{2}{3}h\)	\(I_{yz}=\frac{1}{72}abh^2\)	\(I_{\overline{\overline{zz}}}=\frac{1}{12}bh^3\)

Trapezoid

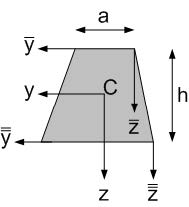
Fig. 3.4 Cross-section of a trapezoid shape.

Table 3.6 Section parameters for trapezoid cross-sections.

Area, centre of gravity	Moments of intertia own	other
\(A=\frac{1}{2}(a+b)h\)	\(I_{zz}=\frac{1}{36}\frac{a^2+4ab+b^2}{a+b}h^3\)	\(I_{\overline{zz}}=\frac{1}{3}bh^3\)
\(\bar{y}_C=\frac{1}{3}\frac{a+2b}{a+b}h\)		\(I_{\overline{\overline{zz}}}=\frac{1}{12}(a+3b)h^3\)
\(\bar{z}_C=\frac{2}{3}h\)

Circle

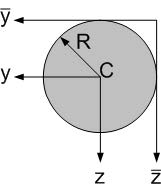
Fig. 3.5 Cross-section of a circle shape.

Table 3.7 Section parameters for circle cross-sections.

Area, centre of gravity	Moments of intertia own	other
\(A=πR^2\)	\(I_{yy}=I_{zz}=\frac{1}{4}R^4\)	\(I_{\overline{yy}}=I_{\overline{zz}}=\frac{5}{4}πR^4\)
	\(I_{yz}=0\)	\(I_{\overline{\overline{yz}}}=πR^4\)
	\(I_p=\frac{1}{2}πR^4\)

Thick-walled ring

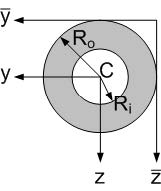
Fig. 3.6 Cross-section of a thick walled ring.

Table 3.8 Section parameters for thick-walled ring cross-sections.

Area, centre of gravity	Moments of intertia own	other
\(A=πR_0^2R_i^2\)	\(I_{yy}=I_{zz}=\frac{1}{4}π(R_0^4-R_i^4)\)
	\(I_{yz}=0\)
	\(I_p=\frac{1}{2}π(R_0^4-R_i^4)\)

Thin-walled ring

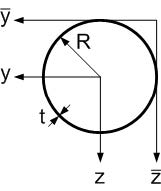
Fig. 3.7 Cross-section of thin walled ring shape.

Table 3.9 Section parameters for thick-walled ring cross-sections.

Area, centre of gravity	Moments of intertia own	other
\(A=2πRt\)	\(I_{yy}=I_{zz}=πR^3t\)	\(I_{\overline{yy}}=I_{\overline{zz}}=3πR^3t\)
	\(I_{yz}=0\)
	\(I_p=\frac{1}{2}πR^3t\)

Half circle

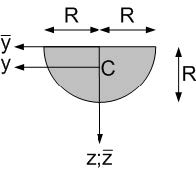
Fig. 3.8 Cross-section of a half circle shape.

Table 3.10 Section parameters for half-circle cross-sections.

Area, centre of gravity	Moments of intertia own	other
\(A=\frac{1}{2}πR^2\)	\(I_{yy}=\frac{1}{8}πR^4\)	\(I_{\overline{yy}}=I_{\overline{zz}}=\frac{1}{8}πR^4\)
\(\bar{y}_C=0\)	\(I_{zz}=(\frac{π}{8}-\frac{8}{9π})R^4\)	\(I_{\overline{\overline{yz}}}=0\)
\(\bar{z}_C=\frac{4}{3π}R\)	\(I_{yz}=0\)

Half thin-walled ring

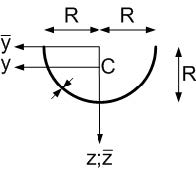
Fig. 3.9 Cross-sectoin of half thin-walled ring.

Table 3.11 Section parameters for half thin-walled ring.

Area, centre of gravity	Moments of intertia own	other
\(A=πRt\)	\(I_{yy}=I_{zz}=\frac{1}{2}R^3t\)	\(I_{\overline{yy}}=I_{\overline{zz}}=\frac{1}{2}πR^3t\)
\(\bar{y}_C=0\)	\(I_{zz}=0\)	\(I_{\overline{yz}}=0\)
\(\bar{z}_C=0\)	\(I_{yz}=0\)

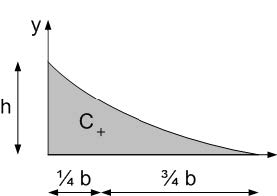
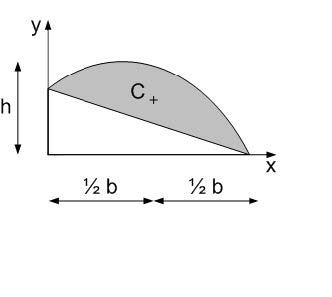
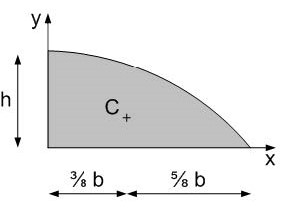
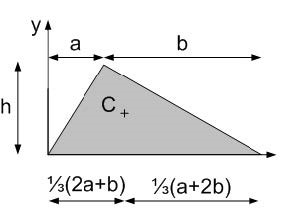
Centre of gravity for moment diagrams